Overview
An important skill in Rocket League is the ability to precisely estimate how long it will take us to reach a certain destination. These time estimates let us answer useful high level questions:
will I be able to reach my destination in time?
will I have enough boost?
will I be able to arrive before my opponent(s)?
is there enough time for me to pick up a boost pad along the way?
if I can reach the destination in time, what speeds can I arrive at?
The answers to these questions determine the decisions we make, so it is essential that our time estimates are as accurate as possible. This article considers how to analyze a particular drivable path in order to answer the questions above.
This analysis does not consider powersliding.
Curves
Let's say I have a curve
In order to calculate the time to traverse a curve, it is helpful to first figure out the length of any section of the curve. To get started, let's zoom in on an arbitrary section of this curve corresponding to the parameter values
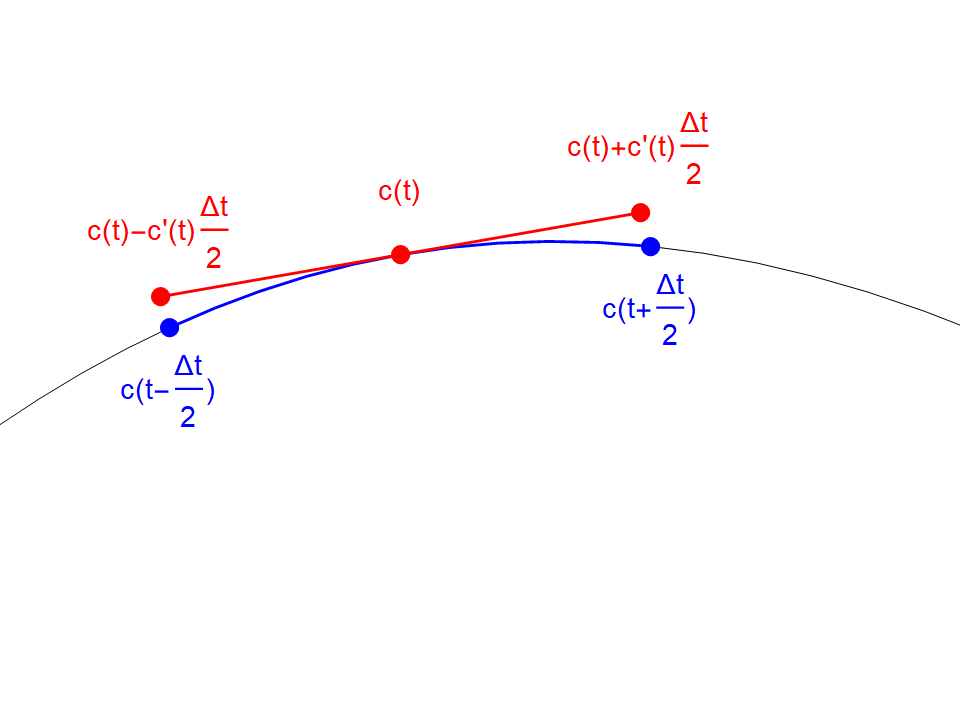
In blue, we have the actual curve segment, whose length we would like to know. In red, we use
Simplifying the righthand side of the above gives us:
Now, since this approximation gets better and better for smaller values of
With this in mind, we can use calculus to add up all of these infinitesimally small lengths. Let
In general, this integral cannot be evaluated in closed form, so we have to integrate numerically. This might sound complicated at first, but it just amounts to sampling points along that curve and calculating distances between adjacent points. Note: the total length of the curve is
It is more convenient to reparameterize our original curve in terms of arc length, since that directly tells us how much distance we have covered already and how much we have left. We denote this arc-length-parameterizated curve by
Now that we have a grasp on the arc length of different sections of the curve, we can calculate the time it would require to traverse a small section of it:
where
All that remains is to determine
Aside: Curvature
The curvature,
The relationship between curvature and radius is a reciprocal one:
In 2D, it is also common to associate a sign with the curvature value, to indicate if the curve is bending to the left (positive sign) or to the right (negative sign).
If we have an expression for
If our curve is described by a sequence of points, then a finite difference stencil can be used to approximate the expression above, but I recommend one of the two beautiful constructions from this paper, with the relevant excerpt below (note, they use
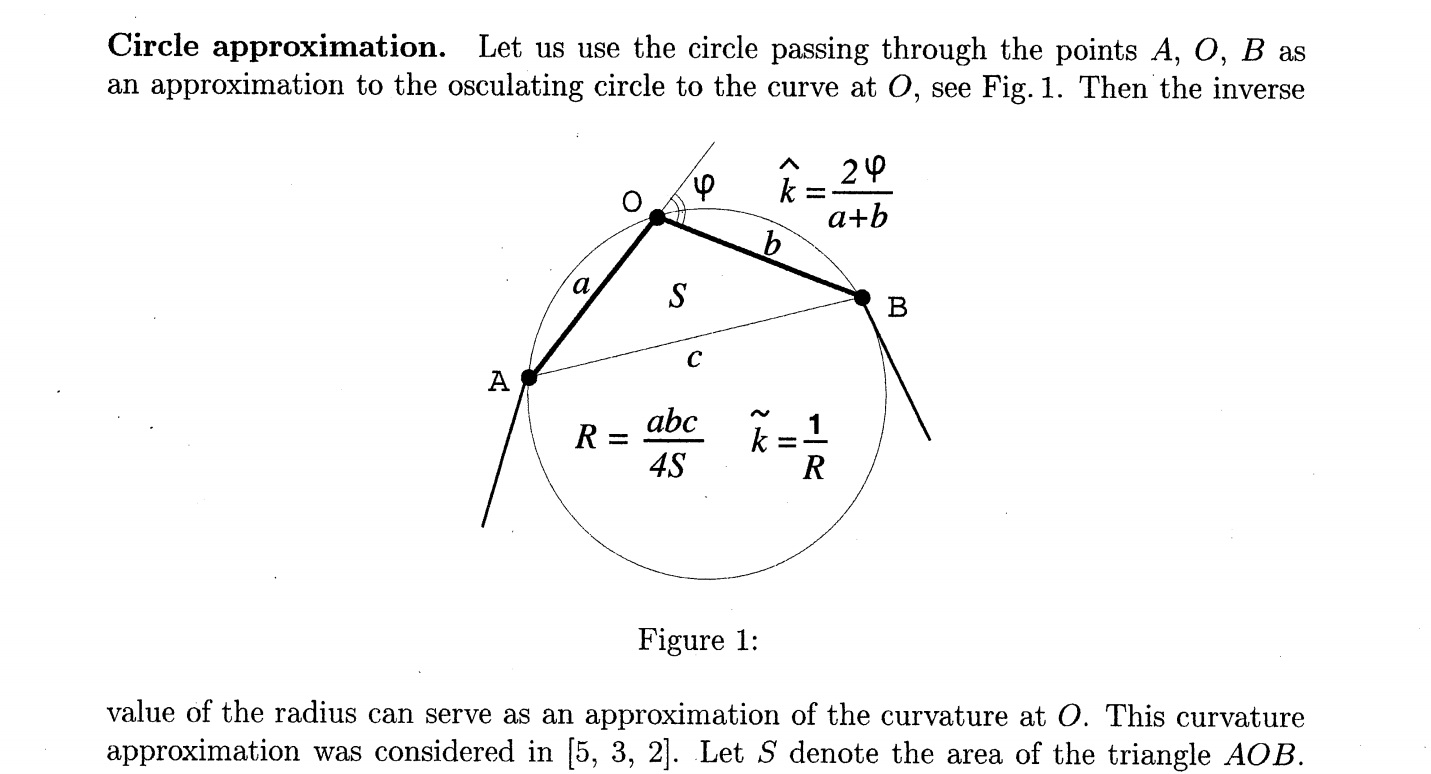
Approximating
The shape of the curve imposes constraints on how fast the car can be travelling instantenously. In another post, we showed that the maximum curvature,
With this in mind, a reasonable first guess for the optimal speed plan,
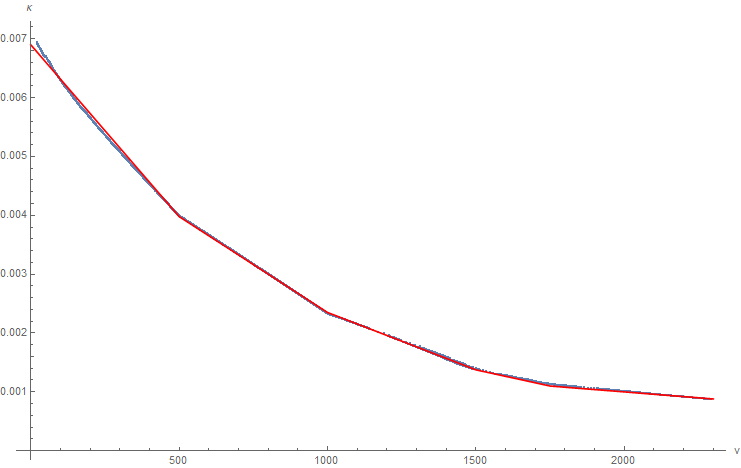
Let's see what a simulation of this assumption looks like, when applied to the example path from earlier (using actual the actual curvature data from Rocket League):
From the plot of
So, let's go back and modify our model to try and include these acceleration constraints from the dynamics of the car.
A Better Approximation for
In this post, we showed how different controls affect the car's acceleration when driving. For this analysis, we only care about braking and boosting, since those are the optimal ways to change our speed the fastest.
For a straightaway, the plot below shows the relationship between speed and distance traveled when boosting (yellow) and braking (blue):
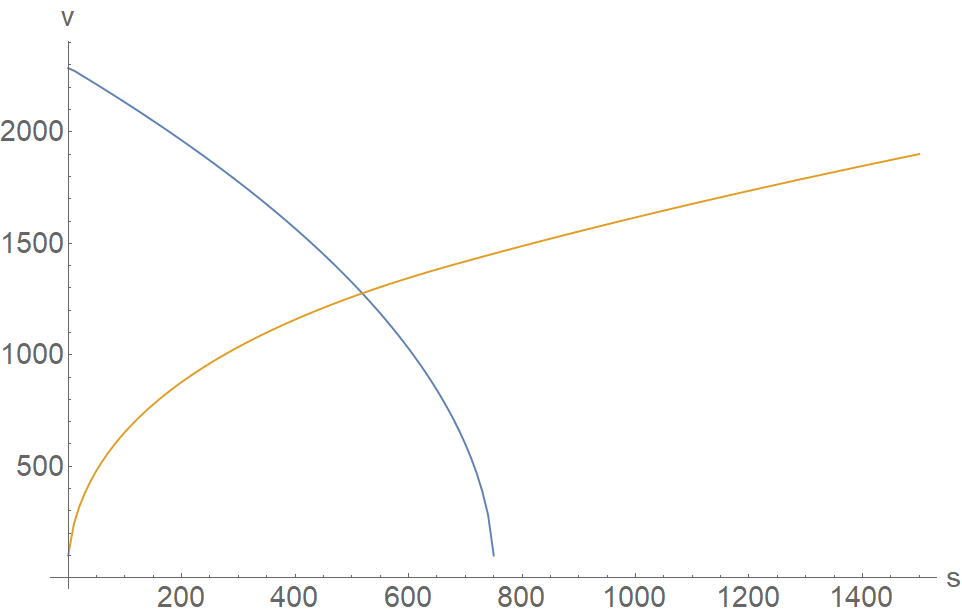
We can use this information to improve our estimate of
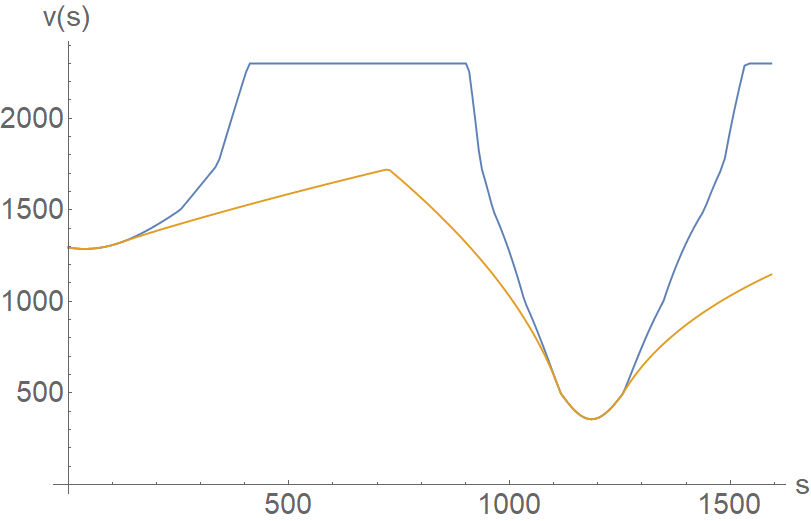
By reading this plot, we can see that the optimal time of traversal involves boosting for the first ~750 units, braking, and then accelerating again once the car is past the turn. So, performing this analysis has found the exact point along the curve where we need to start braking, so that we can still meet the speed requirements of the curve. Additionally, it tells us the maximum possible value for
Summary
In this post we showed how to understand and calculate the arc length, curvature, and maximum speeds attainable by a car with speed-dependent turning radius and finite acceleration. The entire procedure is applicable to almost any curve in space, and we can use these quantities to numerically evaluate the integral that estimates the least time to traverse that path.
The planning problem (which path to take) is still an open question, but the ability to analyze a particular path is an essential step toward being able to determine what the optimal path should be.
Additional Considerations
Other accelerations experienced by the car can also be considered with this approach, by generalizing the slope-limiting process for