This post aims to describe an accurate model of the physics behind the collisions of Rocket League, so that players and bot developers might better understand precisely what happens when the car and ball make contact.
Although these notes are presented on this personal website, this work was a collaboration with Nevercast and tarehart (both members of the RLBot community). Additionally, I also want to express my thanks to Bakkes for developing tools that greatly simplified the data collection process for this analysis.
Hitboxes and Collision Detection
Rocket League doesn't use the actual car's geometry to determine when collisions take place, instead they use oriented bounding boxes (OBBs) for each preset type:

Although this geometry doesn't really match the car very well, it is convenient from a programming perspective because it is inexpensive to perform intersection tests on this simple shape. In particular, we can determine if a sphere is contacting the oriented bounding box by first finding the point on the OBB that is closest to the sphere's center, and then check if the distance between those points is less than the radius.
For a general shape, it can be pretty challenging to find the point on that shape that has the least distance to another point of interest. Fortunately, the orthogonality of the face normals on the OBB make it so we can find that nearest point in only a few lines of code.
Here's one possible implementation of a way to find that nearest point:
xstruct sphere{ vec3 center; float radius;};
struct obb{ vec3 center; vec3 half_width; mat3 orientation;};
vec3 nearest_point_on_obb(const obb & a, const vec3 b) {
// get the local coordinates of b vec3 b_local = dot(b - a.center, a.orientation);
// clip those coordinates to find the closest point (in local coordinates) vec3 closest_local = vec3{ fminf(fmaxf(b_local[0], -a.half_width[0]), a.half_width[0]), fminf(fmaxf(b_local[1], -a.half_width[1]), a.half_width[1]), fminf(fmaxf(b_local[2], -a.half_width[2]), a.half_width[2]) };
// transform back to world coordinates return dot(a.orientation, closest_local) + a.center;
}
bool intersect(const obb & a, const sphere & b) { vec3 p = nearest_point_on_obb(a, b.center); return (norm(p - b.center) <= b.radius);}
Detailed information about hitbox dimensions and offsets for each preset type can be found here, courtesy of halfwaydead. Additionally, his video on hitboxes (and everything else on his channel) is also highly recommended.
Now that we have a way to detect when a collision happens, how does it affect the trajectory of the ball?
Relevant Physics of Rigid Body Collisions
If a car collides with the ball, we need to know the following information to predict the outcome of the collision:
Some other useful notation:
A symbol's subscript will be used to distinguish between quantities belonging to the car and ball (either 'c' for car or 'b' for ball). e.g.
When objects collide, they exert (equal and opposite) forces on each other to prevent interpenetration. In general, there can be many points of contact (each with its own force), but the problem we care about is simple: a sphere hitting a box. In this case, the contact can be reasonably approximated by a force applied a single point. If we knew that force,
So, the velocity change only depends on the impulse itself, not where it is applied. In contrast, the change in angular velocity cares about where that force is being applied, and the matrix
All that remains is to find an expression that tells us how to compute the appropriate value of
In Rocket League, this
Impulse from the Physics Engine
This impulse from the physics engine is modeled as coming from an inelastic rigid-body collision with Coulomb friction.
Intuitively, the 'inelastic collision' part of the model means that the impulse
So, the inelastic collision model demands that
Group similar terms and solve for
So, when the dust settles, we are left with a 3 by 3 system of linear equations. This system can be solved to determine the impulse:
where the matrix
The Coulomb friction model says that the maximum allowable frictional force for the collision is proportional to the normal component of
This constraint is enforced by taking the impulse that comes from the inelastic collision model above, and rescaling
I hope to release a complete reference implementation of this procedure in C++ soon.
Impulse from Psyonix
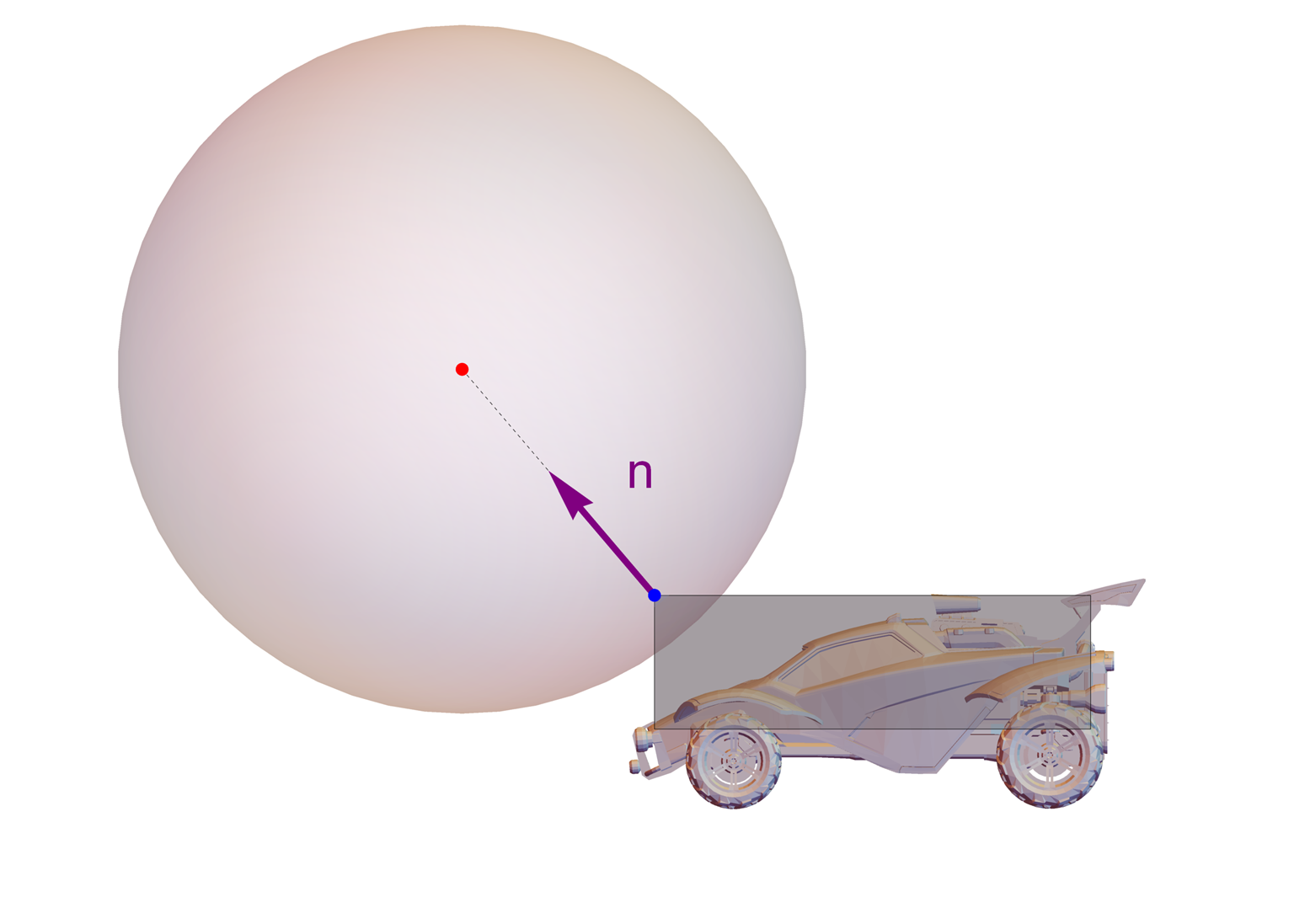
In order to tune the feel and control of the collisions in Rocket League, Psyonix applies an additional impulse to the center of ball (here
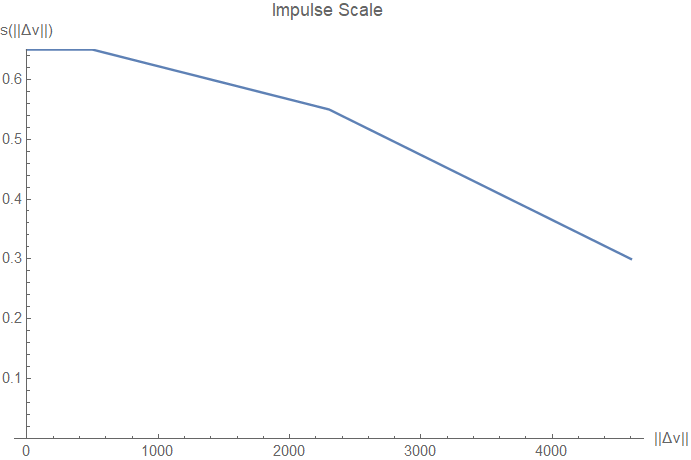
This impulse is simple to describe, as it is given explicitly in terms of only the positions and velocities between the car and ball. Its value is given by:
where
xxxxxxxxxxvec3 f = car.forward();vec3 n = ball.position - car.position;n[2] *= 0.35f;n = normalize(n - 0.35f * dot(n, f) * f);and the scaling function
Oddly enough, this part of the collision violates Newton's 3rd Law of Motion, since Psyonix applies this impulse to the ball without applying an equal and opposite impulse to the car. So, each time you hit the ball in Rocket League, momentum is not conserved!
Example Predictions and Observations
Consider the simple situation where a car approaches the ball, jumps, and dodges forward to make contact (visualization of actual game data, not a simulation):
This scenario was repeated several times by a bot, with different initial separations between the car and ball. It timed the dodges such that when the car contacts the ball, each run has identical velocity and angular velocity, but different orientation. The figures below are closeups of the moment of contact for each run, along with the exact velocity change of the ball compared to the values predicted by the approach described in this article.
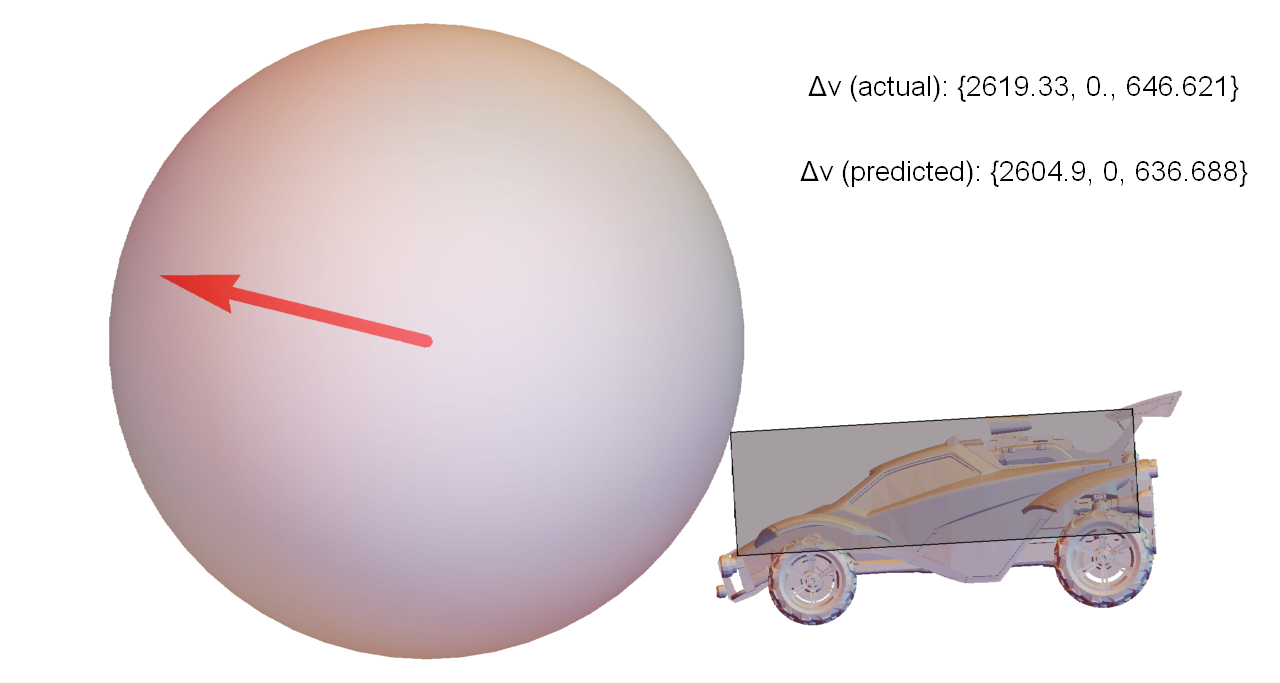
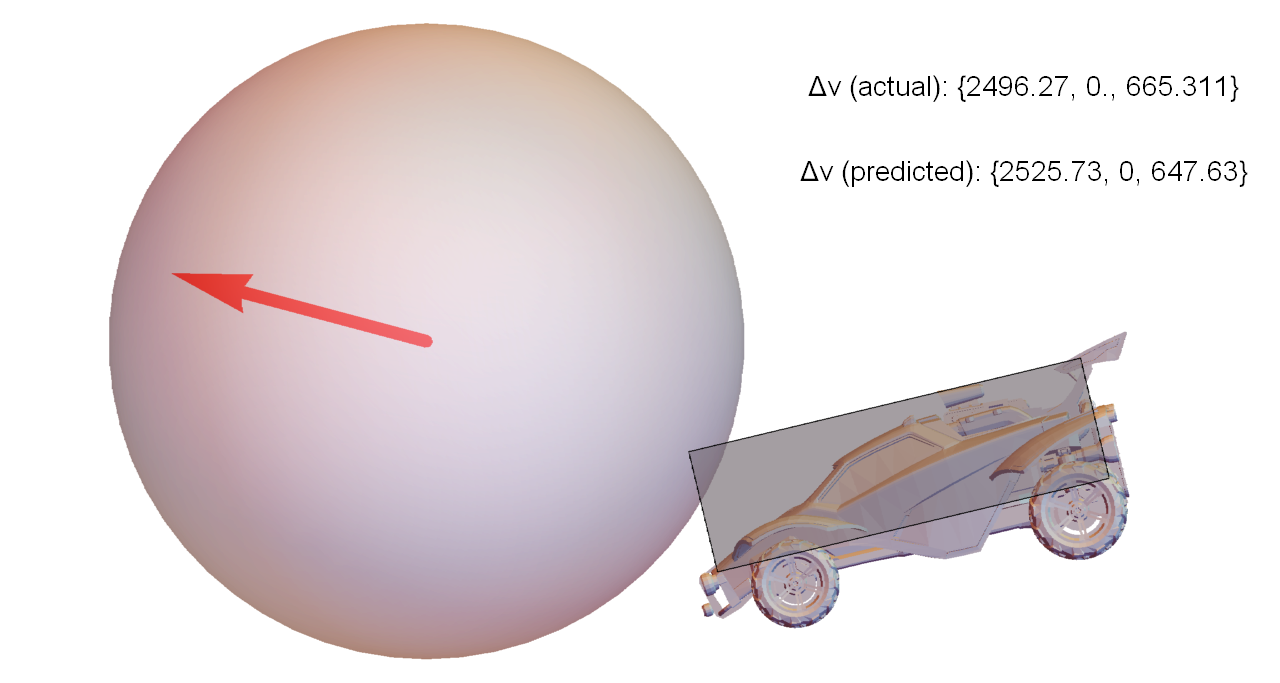
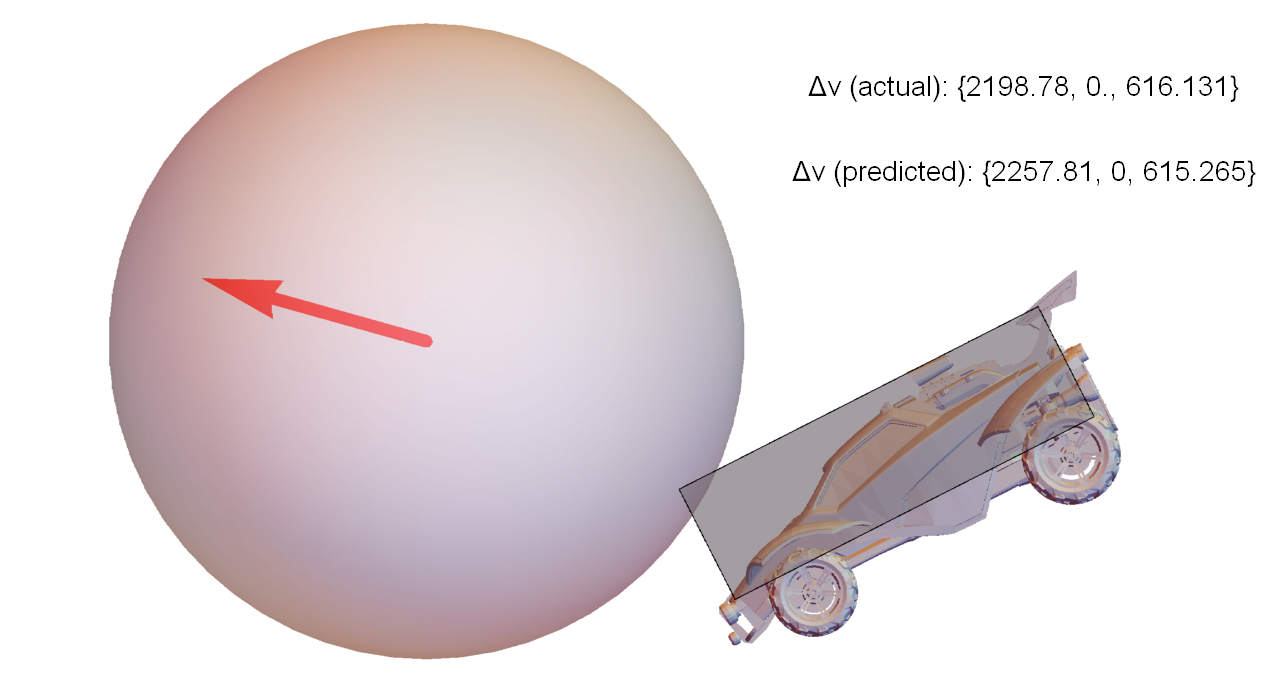
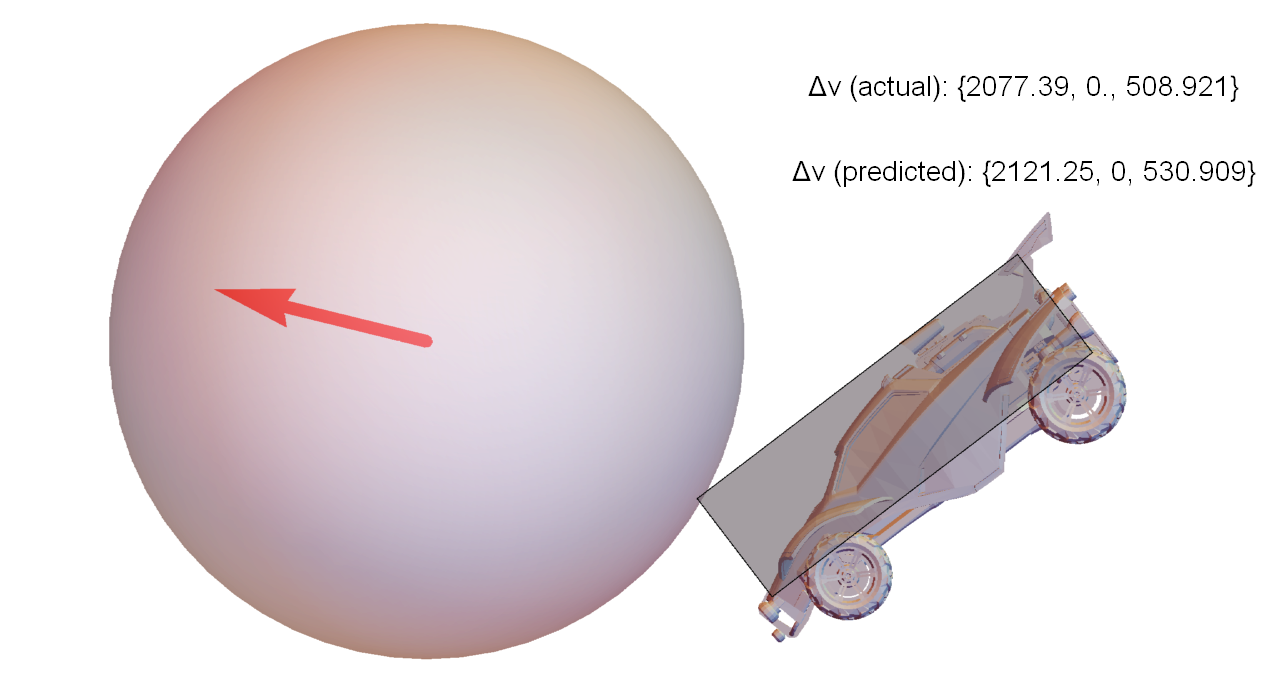
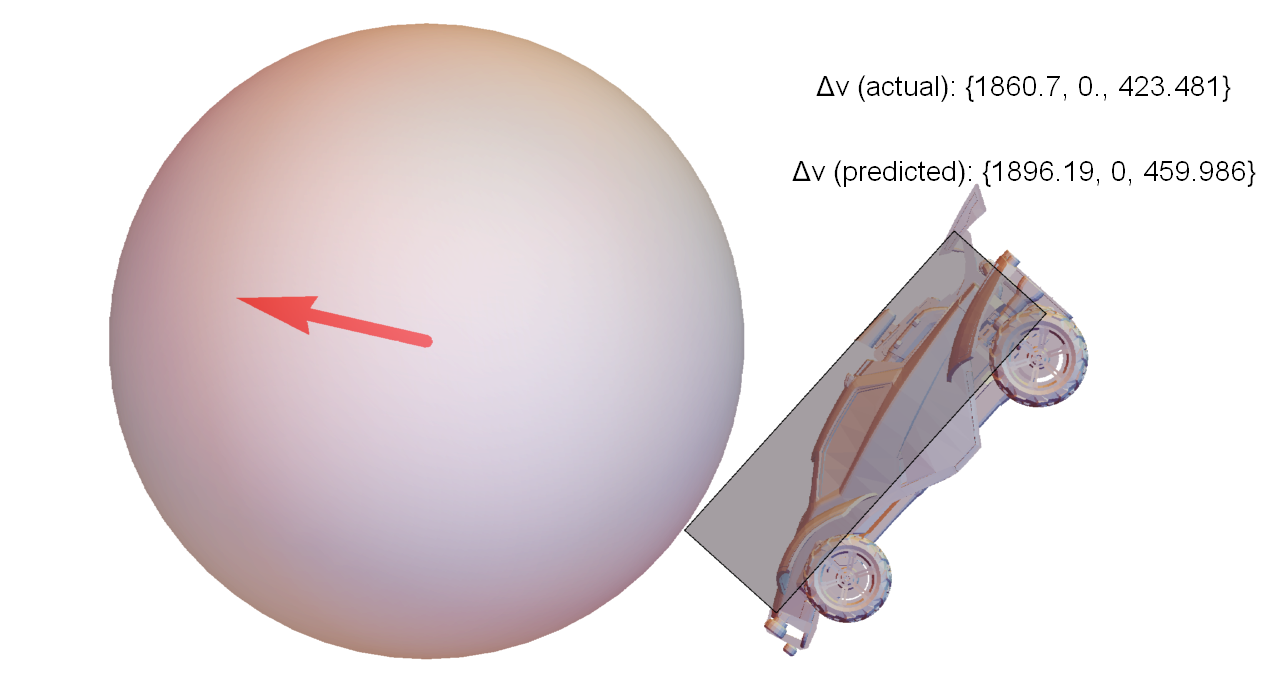
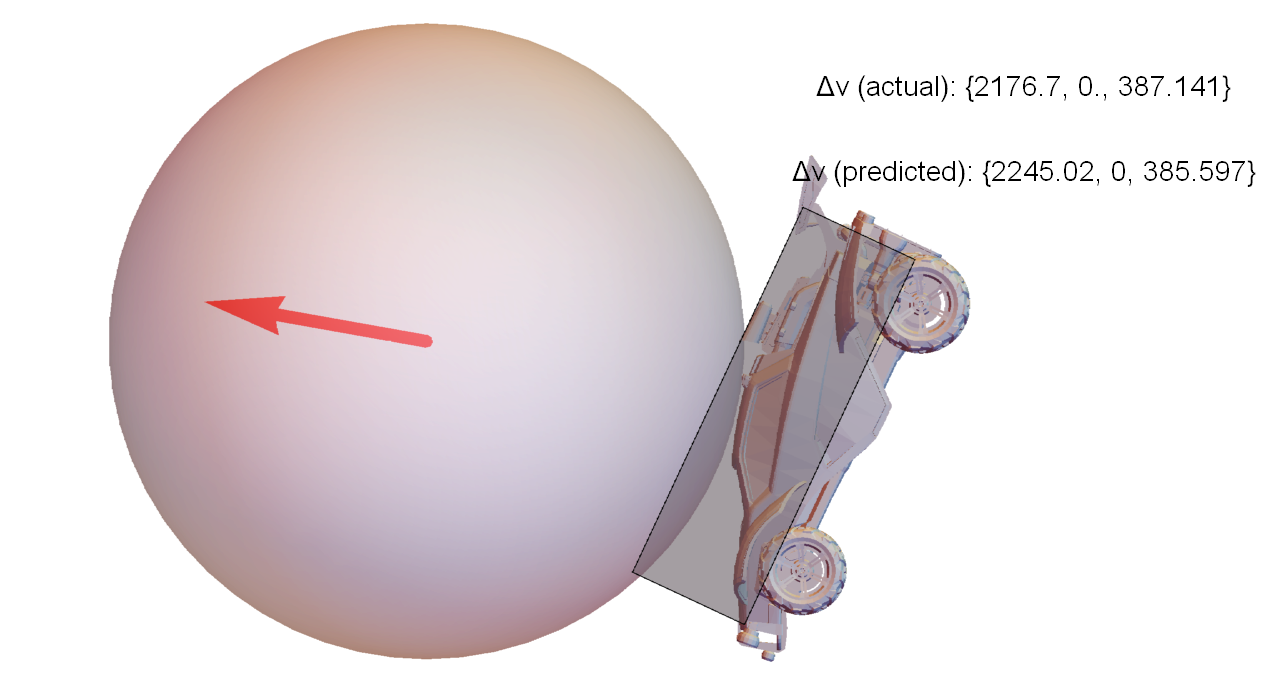
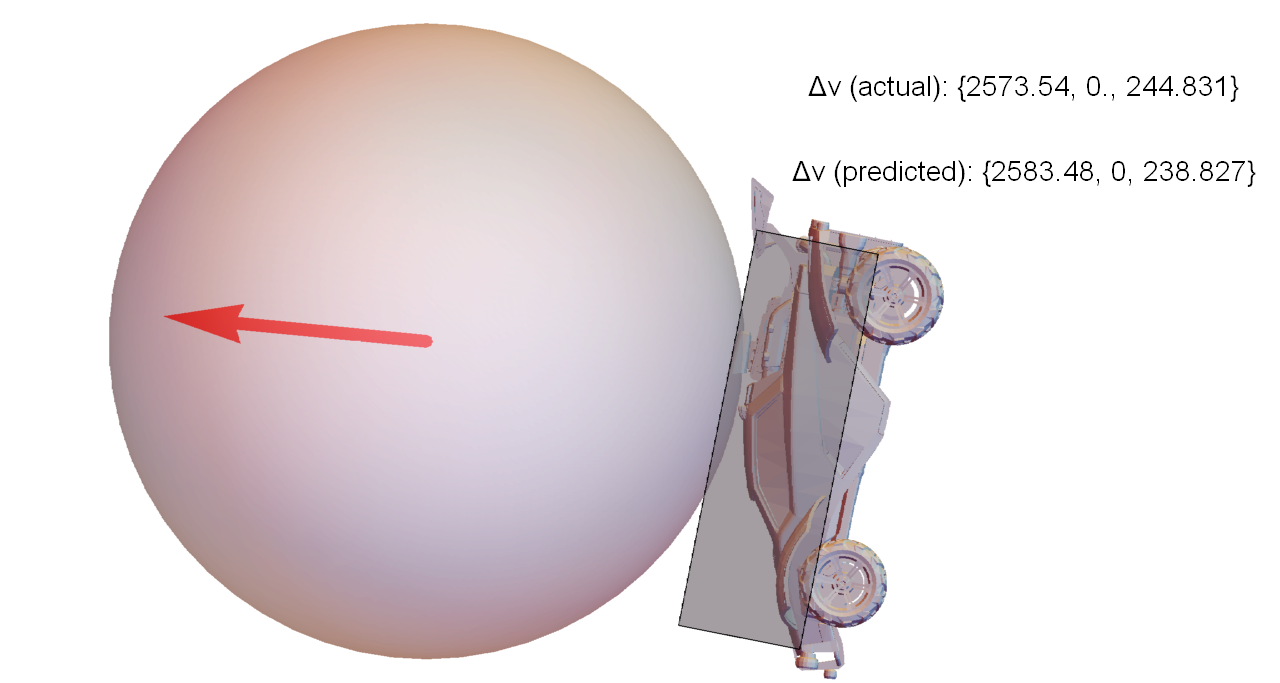
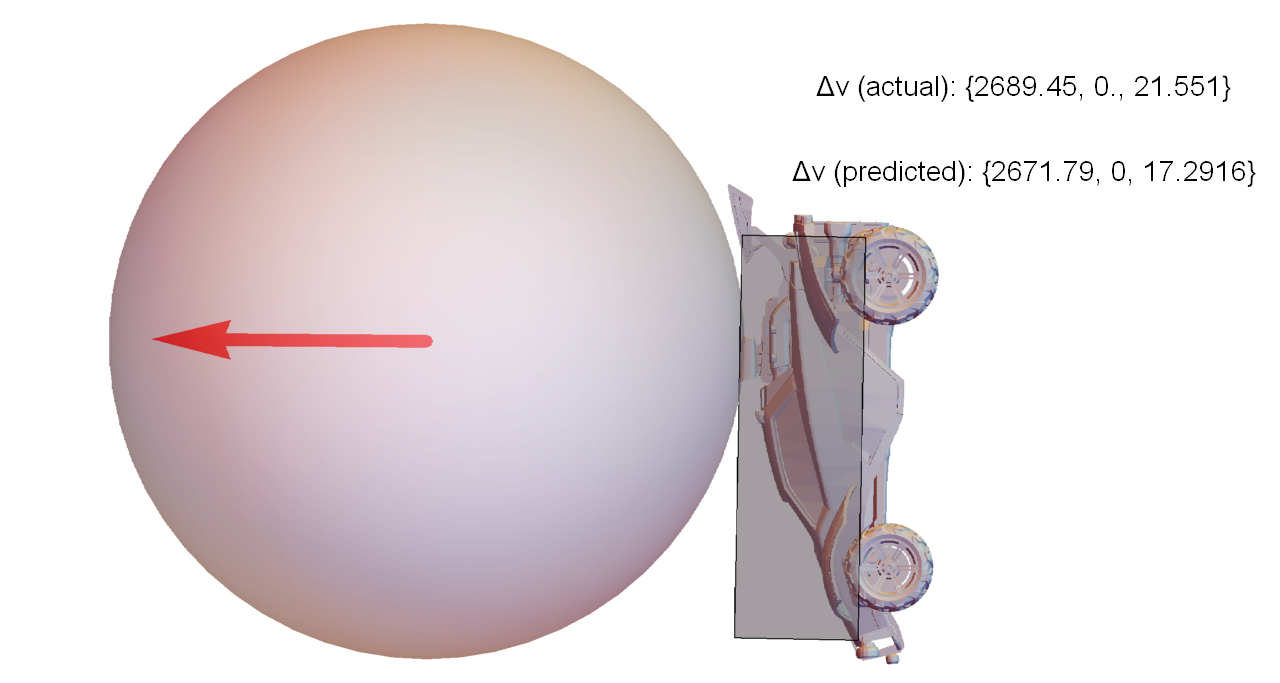
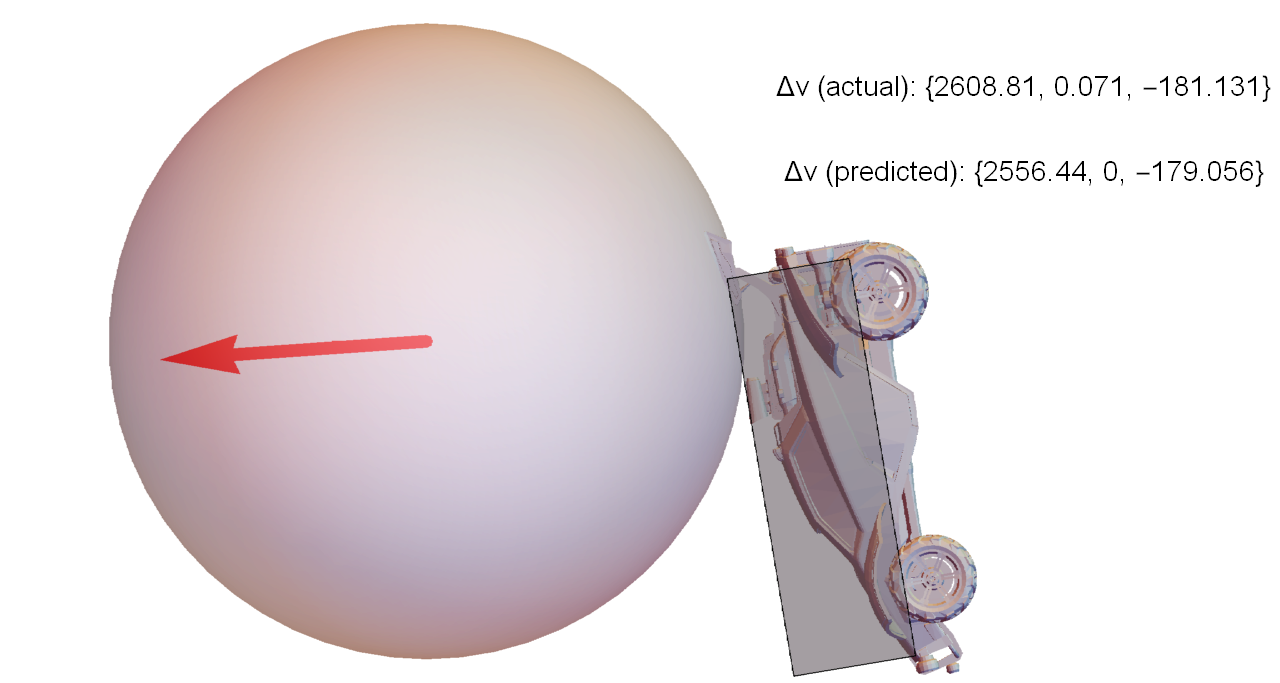
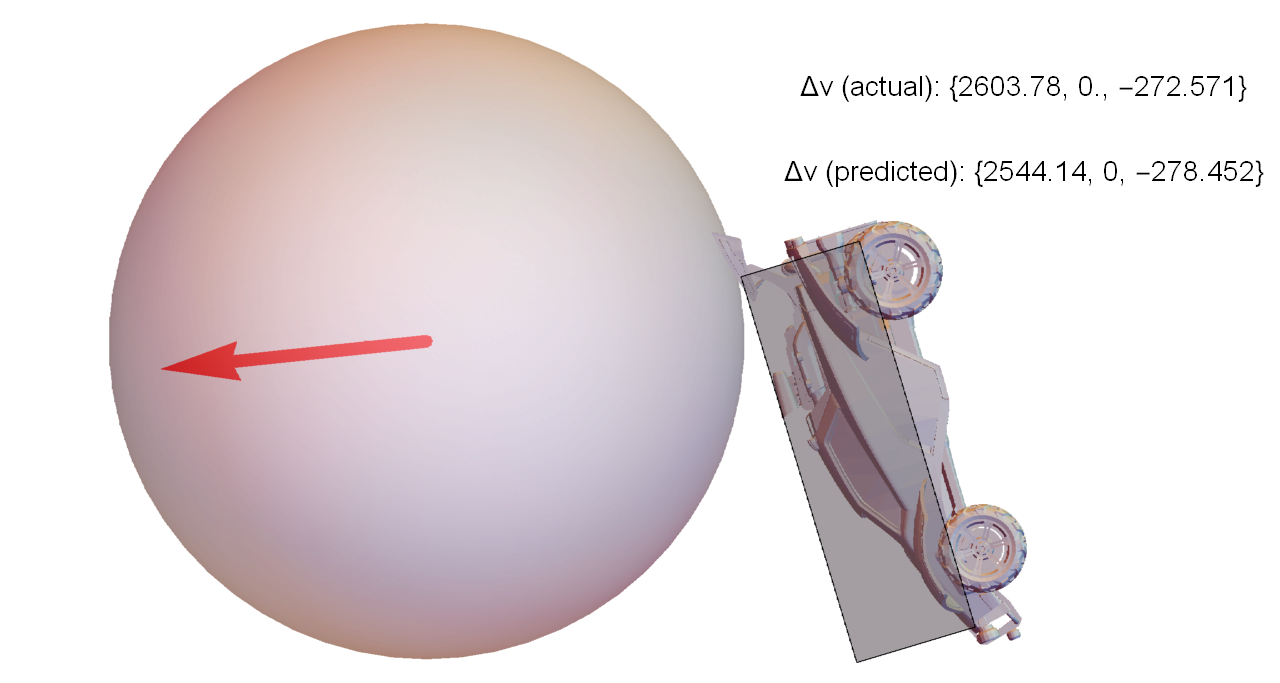
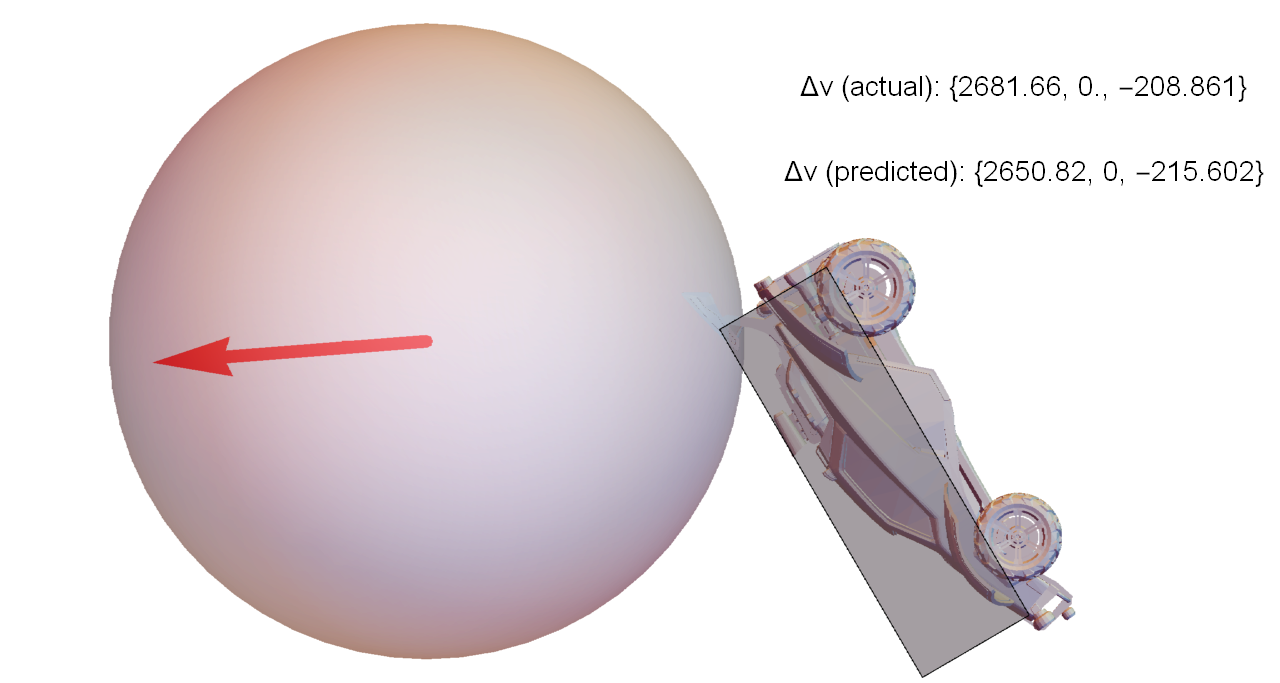
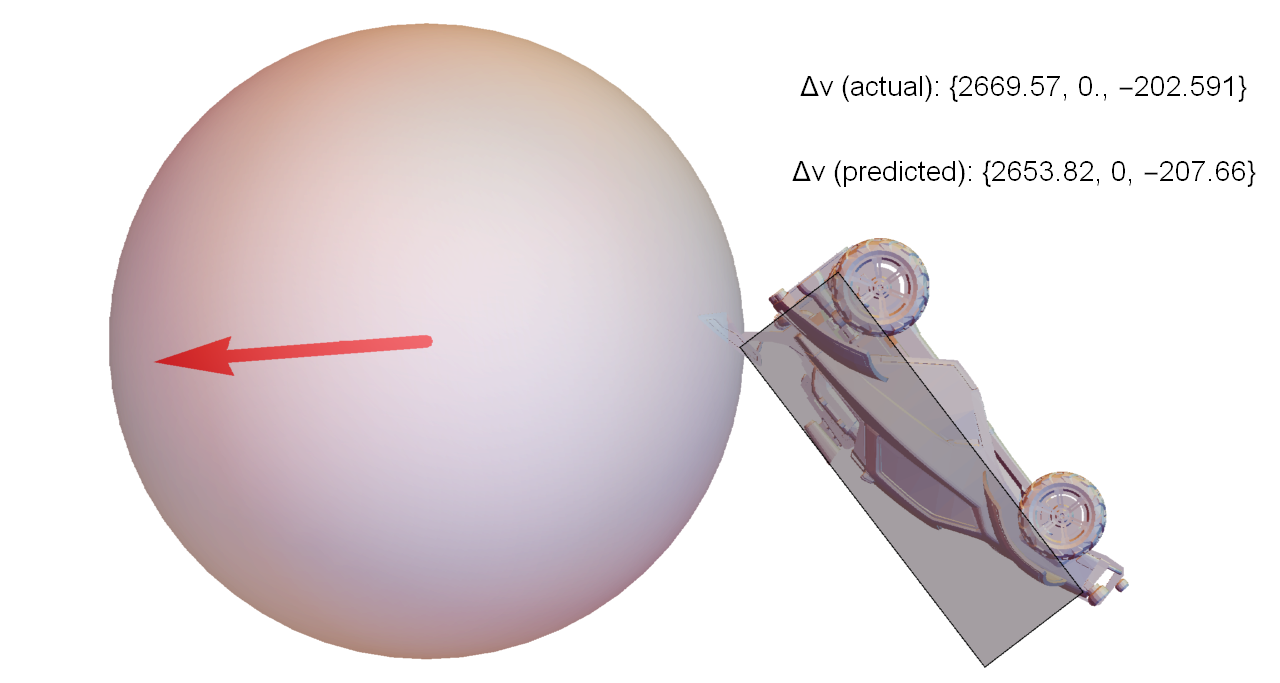
To put these values in perspective, the weakest hit in this set traveled for about 2500 units before hitting the ground again. The strongest hit was 40% faster, and traveled 5200 units (over twice as far).
So, even for a test where almost everything was constrained to be identical, varying the orientation by a few degrees can make a huge difference in the outcome of the collision.
Final Thoughts
This model has been tested on a variety of different types of hits, including dribbling, wall shots, aerial hits, and dodge shots. For these examples, the error in the predictions is small enough to be negligible for practical purposes (on the order of 0.1% to 3% error).
This model is not suitable for wheel hits or pinches!