A good Rocket League bot needs to understand where the ball is going in order to plan what to do. These notes summarize the basic rigid body physics that we need to accurately predict the ball's trajectory.

If you are not interested in any derivations, try skipping ahead to the example implementation, and see it in action (also, it's now available in BakkesMod).

Problem Statement

Consider a scenario where a ball with radius $R$$R$ is about to make contact with a rigid surface with unit normal vector $\mathbf{n}$$\mathbf{n}$. Let $\mathbf{v}$$\mathbf{v}$ be the velocity of the center of mass of the ball, and $\mathit{\omega }$$\boldsymbol{\omega}$ be the angular velocity of the ball.

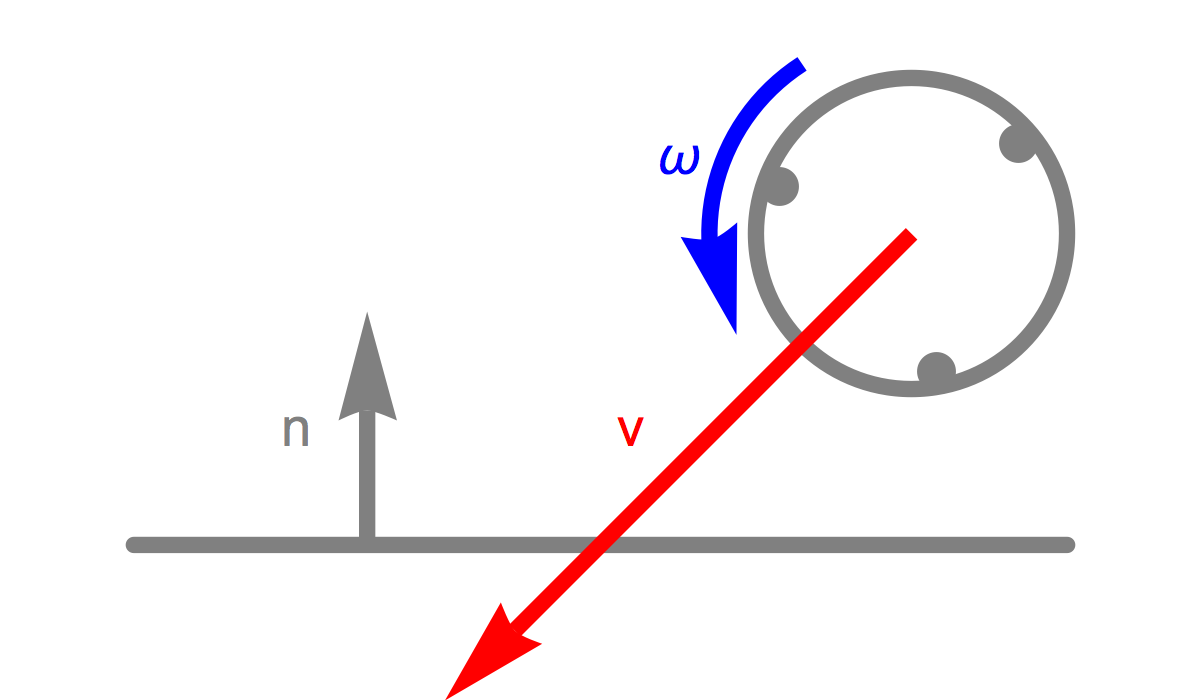
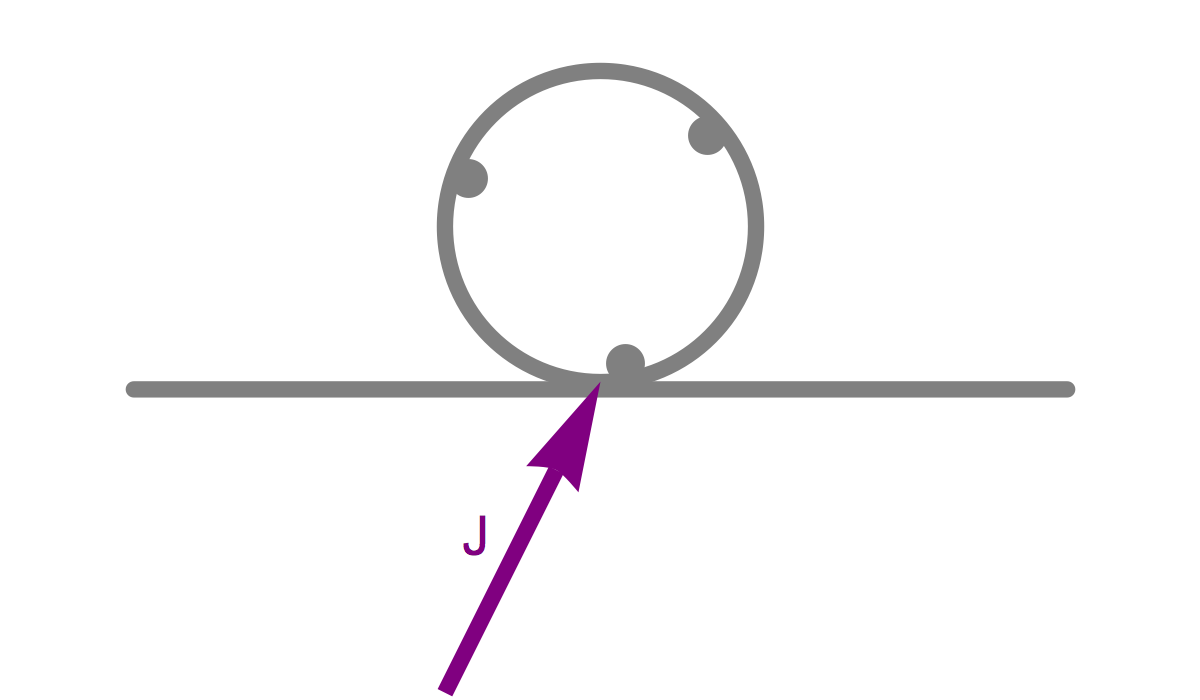
When the ball comes into contact with the rigid surface, it feels an impulse $\mathbf{J}$$\mathbf{J}$ that redirects the ball away from the surface:

To make our calculations work for any surface orientation, we need to express the impulse in terms of its components parallel to the surface, ${\mathbf{J}}_{\parallel }$$\mathbf{J}_{\shortparallel}$, and normal to it, ${\mathbf{J}}_{\perp }$$\mathbf{J}_{\perp}$

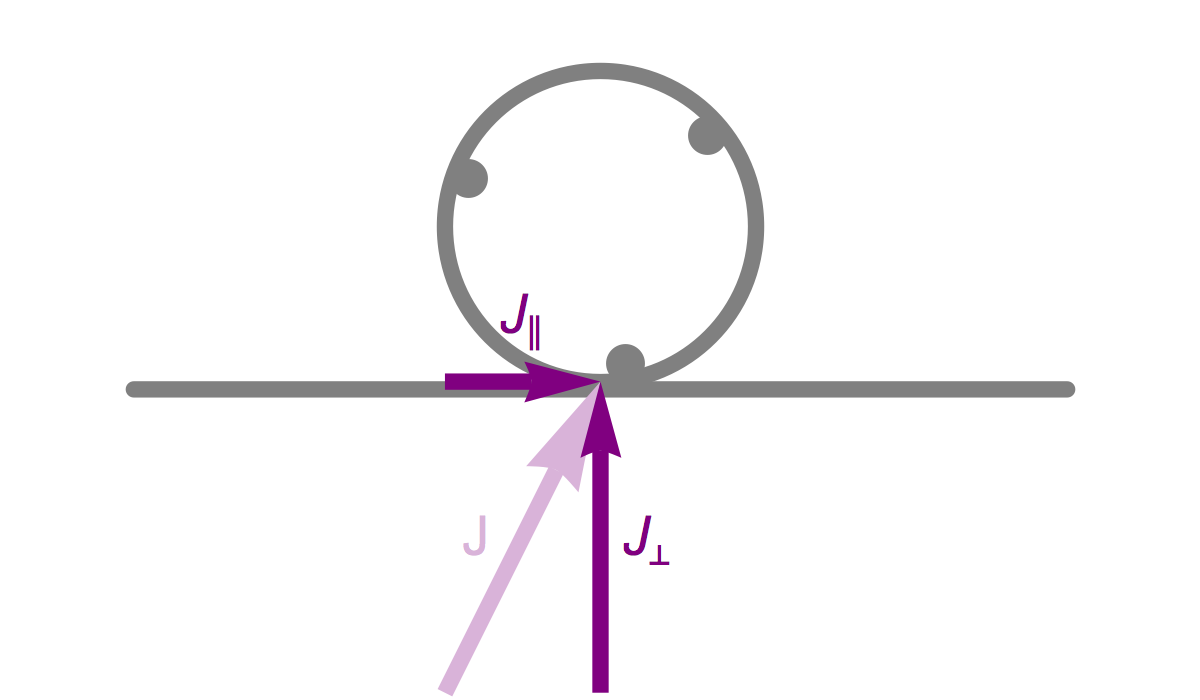
If we knew these components of $\mathbf{J}$$\mathbf{J}$, then we could update the ball's velocity and angular velocity:

where $m$$m$ and $I$$I$ are the ball's mass and moment of inertia (which, for a sphere, can be represented by a scalar value), respectively. Note: since the line of action of ${\mathbf{J}}_{\perp }$$\mathbf{J}_{\perp}$ goes through the center of mass of the ball, it produces no torque. This is why the update procedure for $\mathit{\omega }$$\boldsymbol{\omega}$ only involves ${\mathbf{J}}_{\parallel }$$\mathbf{J}_{\shortparallel}$.

All we need now is a model for how to determine ${\mathbf{J}}_{\parallel }$$\mathbf{J}_{\shortparallel}$ and ${\mathbf{J}}_{\perp }$$\mathbf{J}_{\perp}$.

Normal Impulse

This is the simpler of the two components to figure out. In order to ensure that the ball's corrected velocity will be moving away from the wall, we use the following model

Here, $C_R$$C_R$ is the coefficient of restitution, a number between 0 and 1 that characterizes how much the ball rebounds off of the surface. Empirically, a value of $C_R\approx 0.6$$C_R \approx 0.6$ seems to be a good approximation for Rocket League.

Tangential Impulse

The tangential impulse is related to frictional effects during the moment of contact. There are a number of different frictional models that are commonly used, so it is more challenging to reverse engineer the one being used in Rocket League. Consider the following animation (made from actual data recorded in Rocket League):

The important observation here is that the ball is subjected to a tangential impulse when colliding with the ground, even though its horizontal velocity was initially zero. This indicates that the friction model must be one that opposes the slip velocity, $\mathbf{s}$$\mathbf{s}$, at the point of contact, rather than just the velocity of the ball's center of mass.

Since the surfaces are not moving, the slip velocity is just the velocity of the part of the ball that makes contact with the surface. Like the animation shows, this slip velocity depends on both the ball's angular velocity and the velocity of its center of mass:

The simplest friction model of this type is one that opposes the slip velocity, linearly:

Final notes

Although these expressions include the mass $m$$m$ and moment of inertia $I$$I$, we can't directly measure these values from observations of a ball bouncing. Luckily, it turns out we don't need to know their values to make accurate predictions about the dynamics of the ball.

This provides the description of how to update the ball's velocity and angular velocity, but to make good predictions we also need an appropriate time integrator, and a way to detect which surfaces the ball hits.

Example Implementation

​x
const double R = 91.25;
const double Y = 2.0;
const double mu = 0.285;
const double C_R = 0.6;
const double A = 0.0003;

struct state {
  vec3 x; // position
  vec3 v; // velocity
  vec3 w; // angular velocity
};

state bounce(state current, vec3 n) {
   
  vec3 v_perp = dot(current.v, n) * n;
  vec3 v_para = current.v - v_perp;
  vec3 v_spin = R * cross(n, current.w);
  vec3 s = v_para + v_spin;
   
  double ratio = length(v_perp) / length(s);
   
  vec3 delta_v_perp = - (1.0 + C_R) * v_perp;
  vec3 delta_v_para = - fmin(1.0, Y * ratio) * mu * s;
   
  return state{
    current.x,
    current.v + delta_v_perp + delta_v_para,
    current.w + A * R * cross(delta_v_para, n)
  };  
   
}

Example Predictions

These plots compare actual ball trajectories recorded in Rocket League (solid lines) to the predicted trajectories computed with this model of ball bounce physics, given only the initial conditions (dashed lines). These plots are generated from data file "episode_000218.csv" in the dataset provided at the top of this page.

Ball locations, as a function of time (in frames):

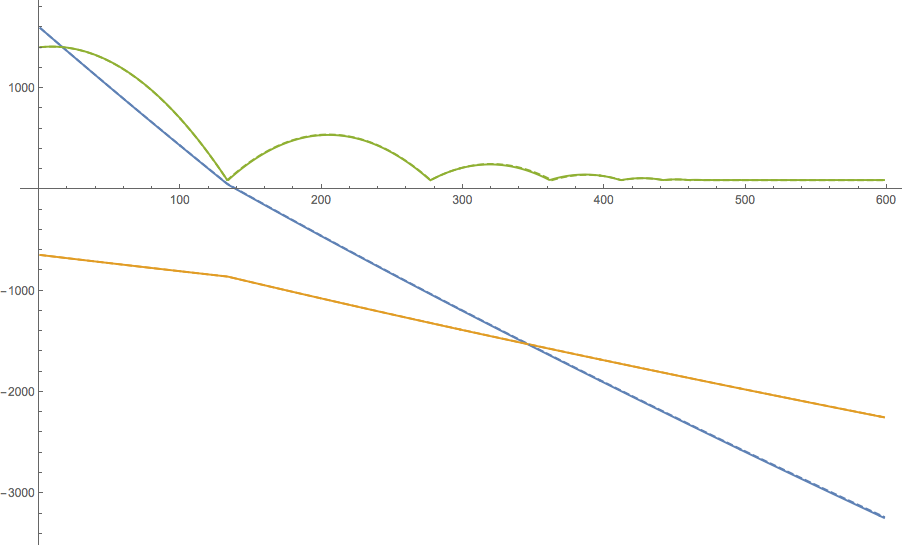
Ball velocities, as a function of time (in frames):

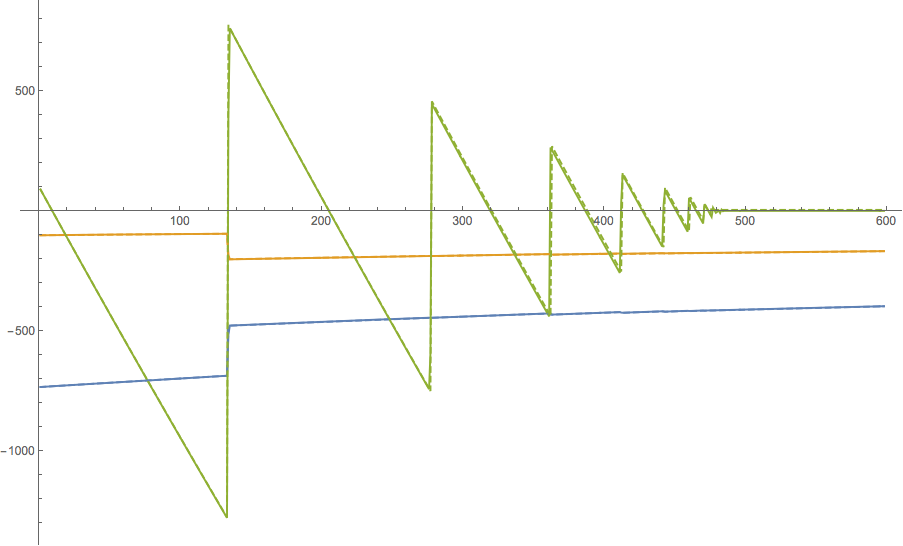
Ball angular velocities, as a function of time (in frames):

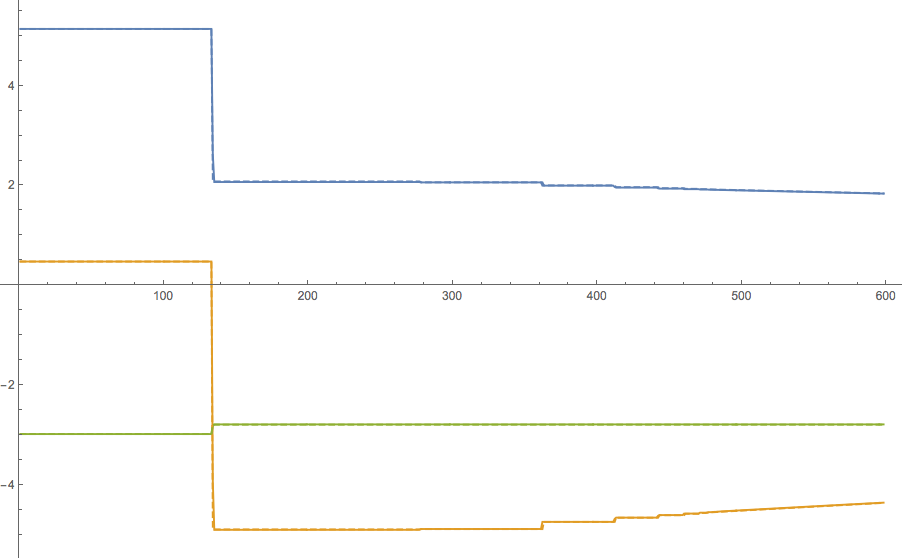
Note: in real time, 600 steps is about 10 seconds. The following are numerical values for the state after 10 seconds of prediction (quantities with a tilde), compared to their exact values (quantities without tilde):

So, it is possible to predict the ball's motion many seconds in advance, with accurate results. Other improvements are still possible, as it looks like Rocket League may explicitly zero out vertical velocity when rolling, etc.