Templated FEM kernels: Benefits and Drawbacks

Many of the low-level FEM kernels in mfem have the following form:

template <int T_D1D = 0, int T_Q1D = 0>
static void SmemPADiffusionApply3D(const int NE, const bool symmetric,
                                   const Array<double> &b_,
                                   const Array<double> &g_, const Vector &d_,
                                   const Vector &x_, Vector &y_,
                                   const int d1d = 0, const int q1d = 0) {
    ...
}

That is, they are function templates where the polynomial order (T_D1D) and quadrature rule (T_Q1D) are template parameters. This has the benefit of making it easy to statically allocate data structures in shared memory (note: MFEM_FORALL_3D is a macro that contains a kernel launch)

  MFEM_FORALL_3D(e, NE, Q1D, Q1D, Q1D, {
      
    const int D1D = T_D1D ? T_D1D : d1d;
    const int Q1D = T_Q1D ? T_Q1D : q1d;
    constexpr int MQ1 = T_Q1D ? T_Q1D : MAX_Q1D;
    constexpr int MD1 = T_D1D ? T_D1D : MAX_D1D;
    constexpr int MDQ = (MQ1 > MD1) ? MQ1 : MD1;
      
    ...
        
    __shared__ double sm0[3][MDQ * MDQ * MDQ];
    __shared__ double sm1[3][MDQ * MDQ * MDQ];
    double(*X)[MD1][MD1] = (double(*)[MD1][MD1])(sm0 + 2);
    double(*DDQ0)[MD1][MQ1] = (double(*)[MD1][MQ1])(sm0 + 0);
    double(*DDQ1)[MD1][MQ1] = (double(*)[MD1][MQ1])(sm0 + 1);
      
    ...
      
  }

The downside is that making this kernel depend on two template parameters means there's potentially about a hundred possible combinations of T_D1D (polynomial order) and T_Q1D (quadrature points per dimension) that a user could request. Covering each of those ~100 possible specializations would mean compiling and optimizing each one independently, having some sort of elaborate case/switch statement to dispatch the appropriate specialization, and making the binary considerably larger.

The approach described above of covering all possible combinations is clearly not practical, and mfem opts for a compromise instead:

• manually curate a set of {T_D1D, T_Q1D} combinations that show up most commonly in practice

• implement a fallback kernel that covers the remaining combinations, with reduced performance

The difference in performance between mfem's templated kernels and the dynamic fallback option is significant, especially for low order:

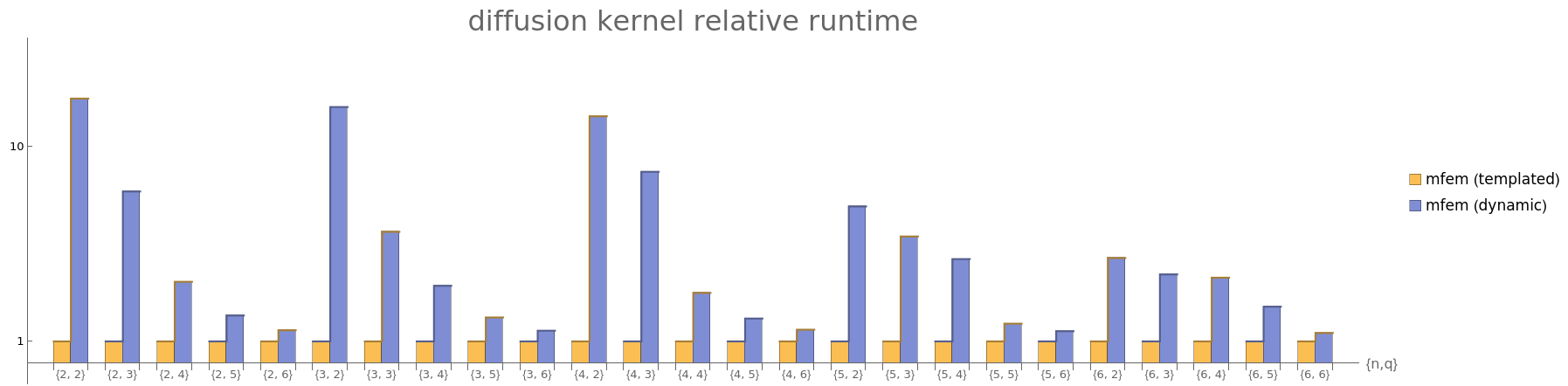
So, although this compromise is preferable to compiling each kernel a hundred times, it still compiles each kernel ~10 times, and admits the possibility of considerable loss of performance if the user requests a kernel that is not part of the curated set.

The question is: why not just implement the kernel where polynomial order and quadrature rules are specified dynamically, but without overallocating shared memory (the approach used by mfem's fallback kernel)?

An Alternative Implementation

The main part of the current mfem kernel implementation that necessitates compile-time knowledge of polynomial order and quadrature rule is the static allocation of shared memory:

__shared__ double sm0[3][MDQ * MDQ * MDQ];
double(*X)[MD1][MD1] = (double(*)[MD1][MD1])(sm0 + 2);
double(*DDQ0)[MD1][MQ1] = (double(*)[MD1][MQ1])(sm0 + 0);
double(*DDQ1)[MD1][MQ1] = (double(*)[MD1][MQ1])(sm0 + 1);
...

So, what if we just allocated the shared memory dynamically?

extern __shared__ double sm0[]; // this is sized at runtime
int offset = 0;
int step = D1D * D1D * D1D;
ndview    X(sm0 + offset, {D1D, D1D, D1D}); offset += step;
ndview DDQ0(sm0 + offset, {D1D, D1D, Q1D}); offset += step;
ndview DDQ1(sm0 + offset, {D1D, D1D, Q1D}); offset += step;
...

where ndview is a non-owning, GPU-compatible multidimensional array class (since C++ notoriously lacks such a container in the standard library). Its full implementation is only 30 lines of code, and is given at the end of the document.

Now that there is no requirement to have the kernel take template parameters, one kernel can cover all of the possible combinations of polynomial order and quadrature rule.

By making this small modification, the performance of the new kernel is close to parity with the templated mfem kernels:

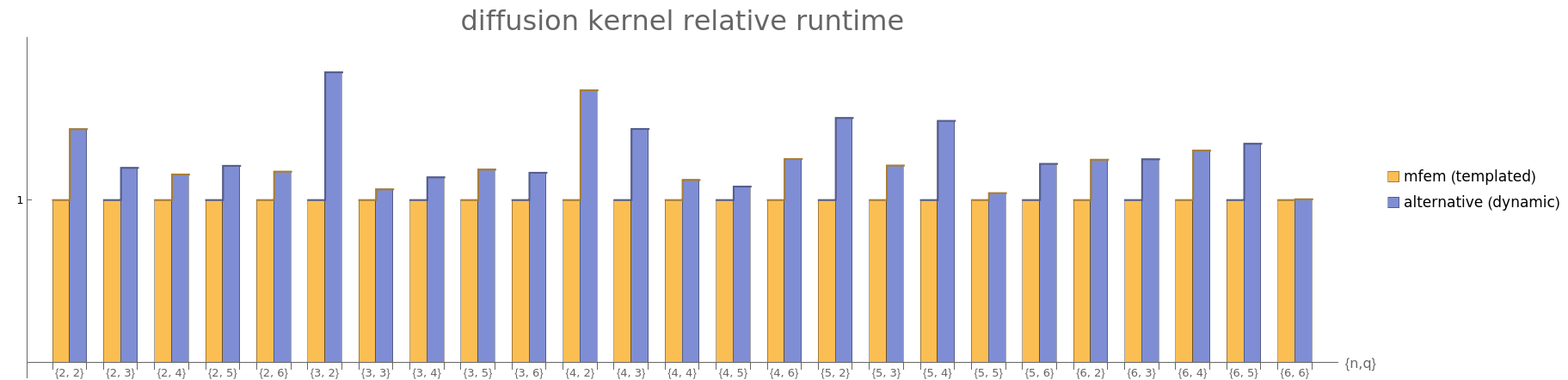
Furthermore, making a few other small modifications (most notably, the possibility of processing multiple elements per thread block) can make the alternative dynamic kernel implementation competitive or better than the templated implementation in mfem:

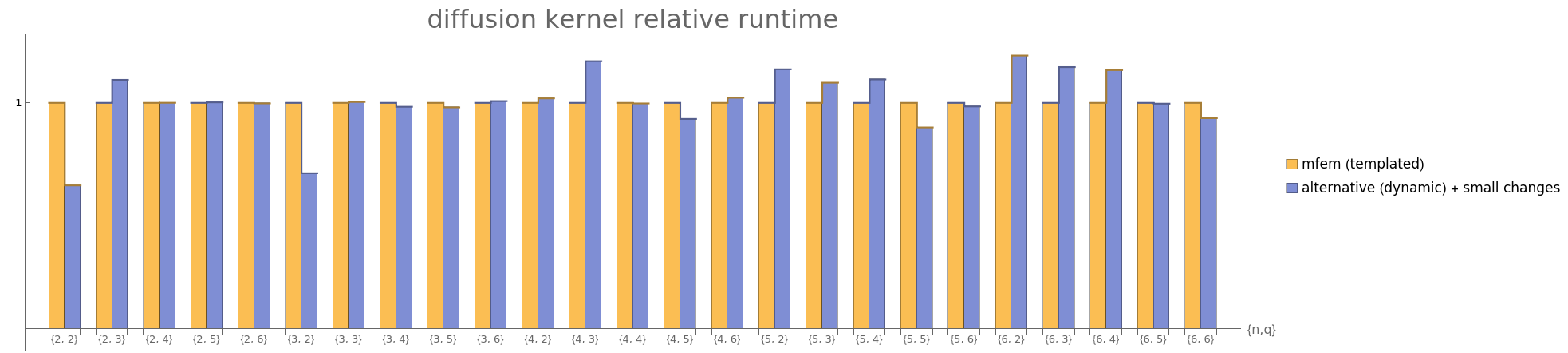
Note: all performance numbers are taken from tests on a NVIDIA GV100 GPU.

Summary

Templates are a powerful tool. They enable developers to make certain information available at compile time, which can reveal additional optimizations that improve performance.

However, that doesn't mean that templates are a requirement for performant code.

In this document, we looked at a real-world example where template parameters were assumed to be necessary for getting the best kernel performance, but that wasn't the case. Refactoring the kernel to use fewer templates significantly reduced binary size and compile time, while retaining performance parity.

The takeaway here isn't to never use templates, but to pick the right tool for the job. Like Chandler Carruth emphasizes in this wonderful talk: given the choice between two equivalent implementations, prefer the simpler abstraction!

ndview Implementation

template < typename T, int rank = 1 >
struct ndview{
  static constexpr auto iseq = std::make_integer_sequence<int, rank>{};

  __host__ __device__ ndview() {}

  __host__ __device__ ndview(T * input, const int (& dimensions)[rank]) {
    data = input;
    for (int i = 0; i < rank; i++) {
      int id = rank - 1 - i;
      shape[id] = dimensions[id];
      strides[id] = (id == rank - 1) ? 1 : strides[id+1] * shape[id+1];
    }
  }

  template < typename ... index_types >
  __host__ __device__ auto & operator()(index_types ... indices) { 
    static_assert(sizeof ... (indices) == rank);
    return data[index(iseq, indices...)];
  }

  template < typename ... index_types >
  __host__ __device__ auto & operator()(index_types ... indices) const { 
    static_assert(sizeof ... (indices) == rank);
    return data[index(iseq, indices...)];
  }

  template < int ... I, typename ... index_types >
  __host__ __device__ auto index(std::integer_sequence<int, I...>, index_types ... indices) const {
    return ((indices * strides[I]) + ...);
  }

  T * data;
  int shape[rank];
  int strides[rank];
};

Portability-Layer Wrapper

One naive way to include dynamic shared memory allocation in a "forall" framework (e.g. RAJA, Kokkos, etc)

#include <cstdio>

enum class Device { CPU, GPU };

template < typename callable >
__global__ void forall_kernel(callable f, int n) {
    int i = threadIdx.x + blockIdx.x * blockDim.x;
    if (i < n) { f(i); } 
}

template < Device device, typename callable >
void forall(callable f, int n) {
    if constexpr (device == Device::CPU) {
        printf("(cpu) forall\n");
        for (int i = 0; i < n; i++) { f(i); }
    } else {
        printf("(gpu) forall\n");
        int blocksize = 128; // in practice, this should be configurable rather than hardcoded
        int gridsize = (n + blocksize - 1) / blocksize;
        forall_kernel<<<gridsize,blocksize>>>(f, n);
        cudaDeviceSynchronize();
    }
}

template < typename callable >
__global__ void forall_kernel_shmem(callable f, int n, int num_bytes) {
    int i = threadIdx.x + blockIdx.x * blockDim.x;
    extern __shared__ char buffer[];
    if (i < n) { f(i, buffer); } 
}

template < Device device, typename callable >
void forall(callable f, int n, int shmem) {
    if constexpr (device == Device::CPU) {
        printf("(cpu) forall, w/ 'shared memory'\n");
        char * buffer = new char[n];
        for (int i = 0; i < n; i++) { f(i, buffer); }
        delete[] buffer;
    } else {
        printf("(gpu) forall w/ shared memory\n");
        int blocksize = 128; // in practice, this should be configurable rather than hardcoded
        int gridsize = (n + blocksize - 1) / blocksize;
        forall_kernel_shmem<<<gridsize,blocksize,shmem>>>(f, n, shmem);
        cudaDeviceSynchronize();
    }
}

int main() {
    auto f1 = [] __host__ __device__ (int i) {
        printf("%d\n", i);
    };

    auto f2 = [] __host__ __device__ (int i, char * buffer) {
        buffer[i] = i * i; // store and use shared memory buffer
        printf("%d, %d\n", i, buffer[i]);
    };
    
    int n = 4;
    forall<Device::CPU>(f1, n);
    forall<Device::GPU>(f1, n);

    int shmem_bytes = 64;
    forall<Device::CPU>(f2, n, shmem_bytes);
    forall<Device::GPU>(f2, n, shmem_bytes);
}

// output: 
// 
// (cpu) forall
// 0
// 1
// 2
// 3
// (gpu) forall
// 0
// 1
// 2
// 3
// (cpu) forall, w/ 'shared memory'
// 0, 0
// 1, 1
// 2, 4
// 3, 9
// (gpu) forall w/ shared memory
// 0, 0
// 1, 1
// 2, 4
// 3, 9