Sum of Integers
It is said (perhaps apocryphally) that while Gauss was in elementary school, he and his classmates were assigned the task of summing the integers from 1 to 100, as a way to keep them busy for a while. To the teacher's surprise, Gauss finished unusually quickly, with the correct answer: 5050. He explained that it was not actually necessary to add all those numbers individually, but that (I'm paraphrasing) you can think of the sum of the first
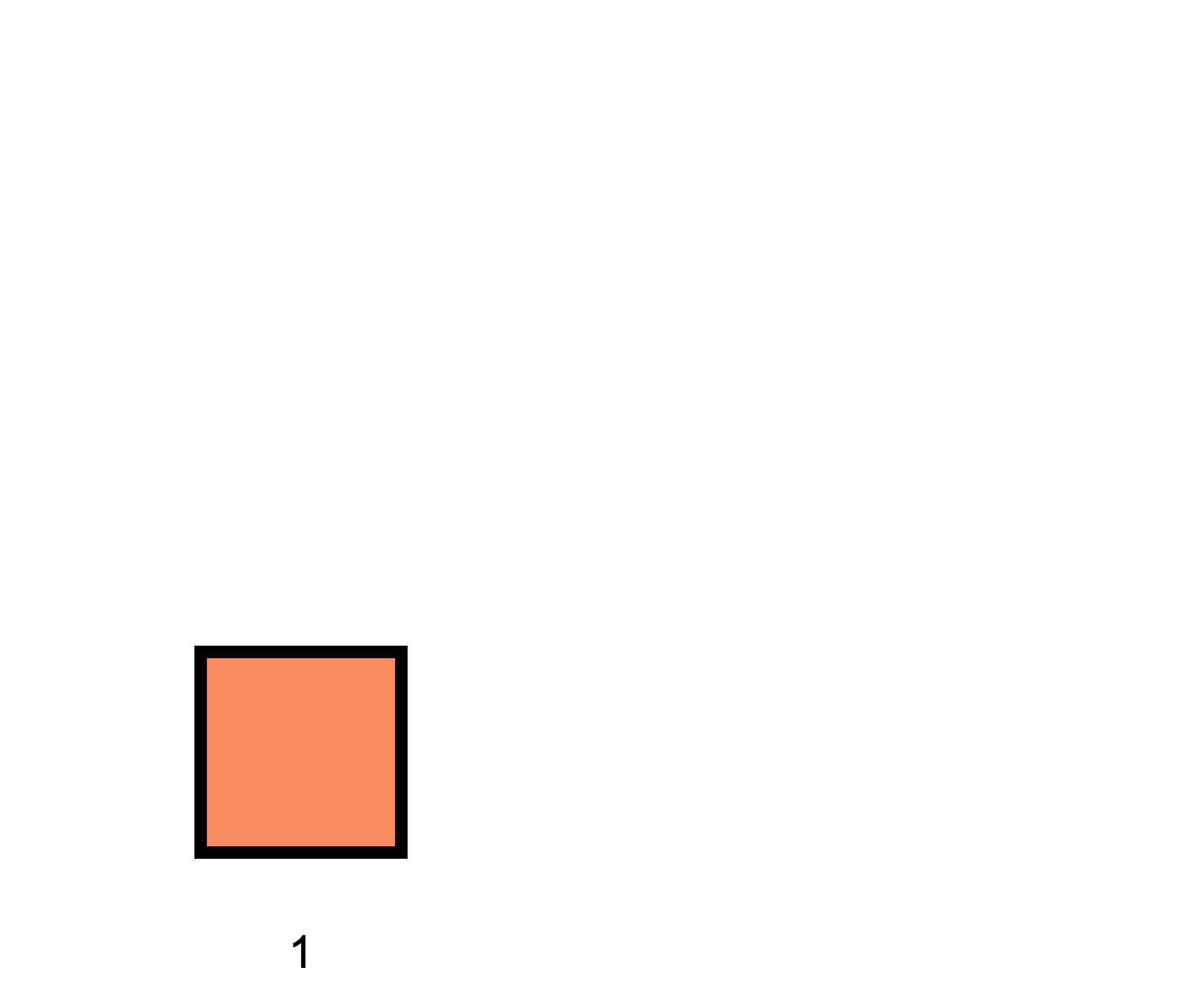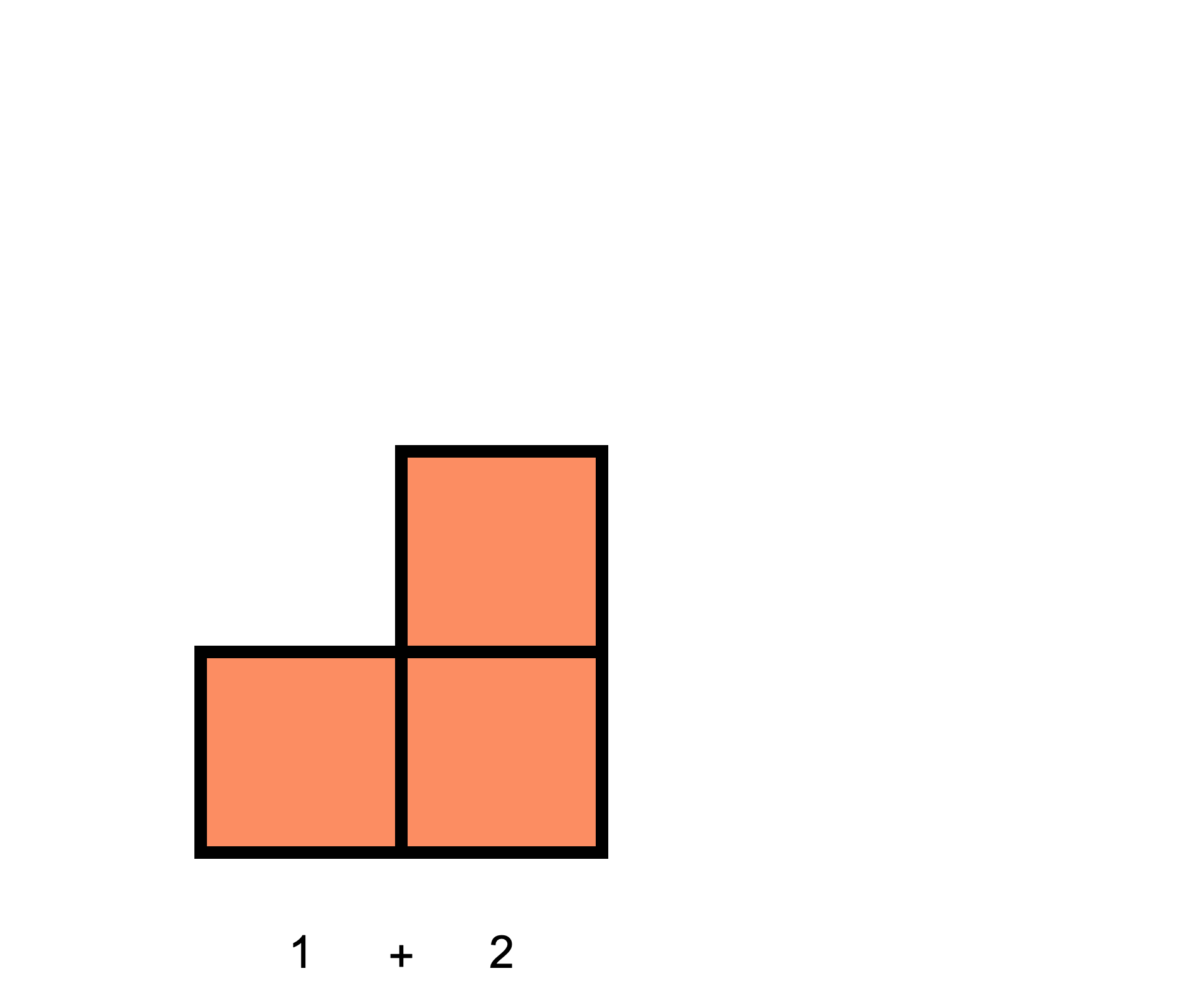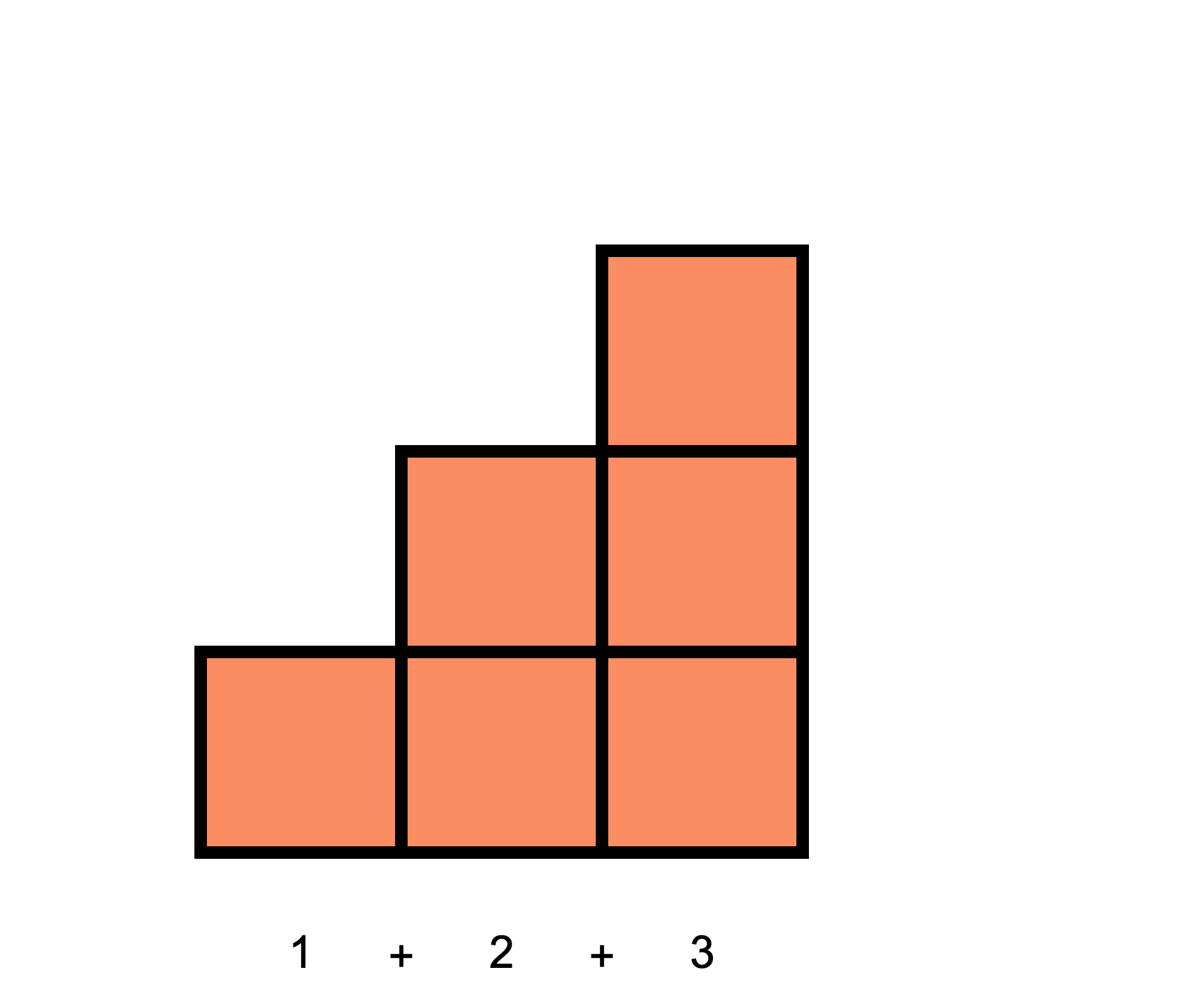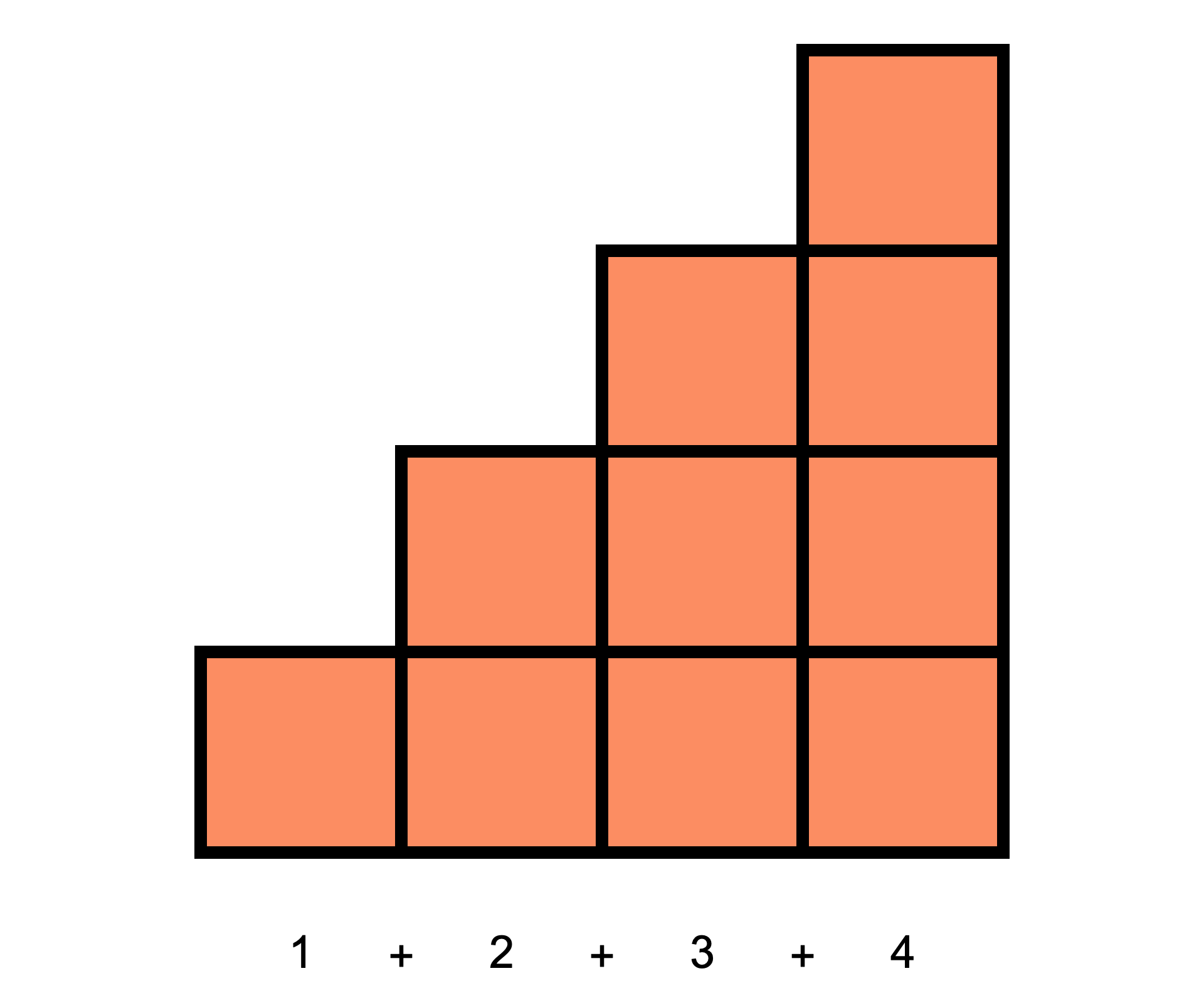
and that two of these "staircases" can be arranged into a rectangle:
So, it must follow that the area of one of them is half the area of the rectangle. This is a geometric interpretation of the algebraic formula for the sum of the first
It's a beautiful explanation, regardless of whether or not the story is true!
Sum of Squares
In calculus, while learning about the formulas for sums of the first
I wondered: is there a similar geometric understanding of these formulas too? It turns out that, for the sum of squares, the answer is yes. Just like before, we can interpret the sum of the squares of the first
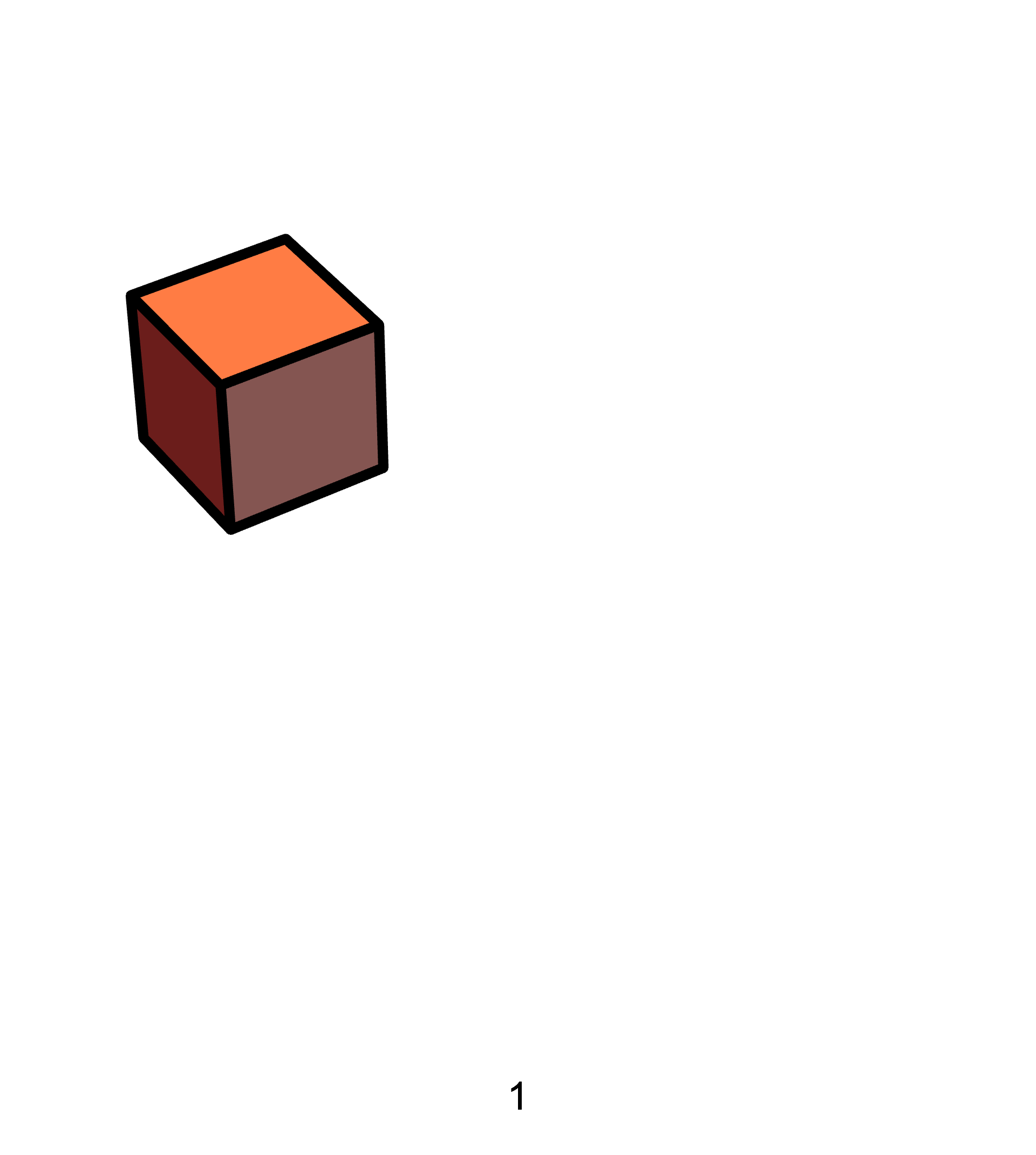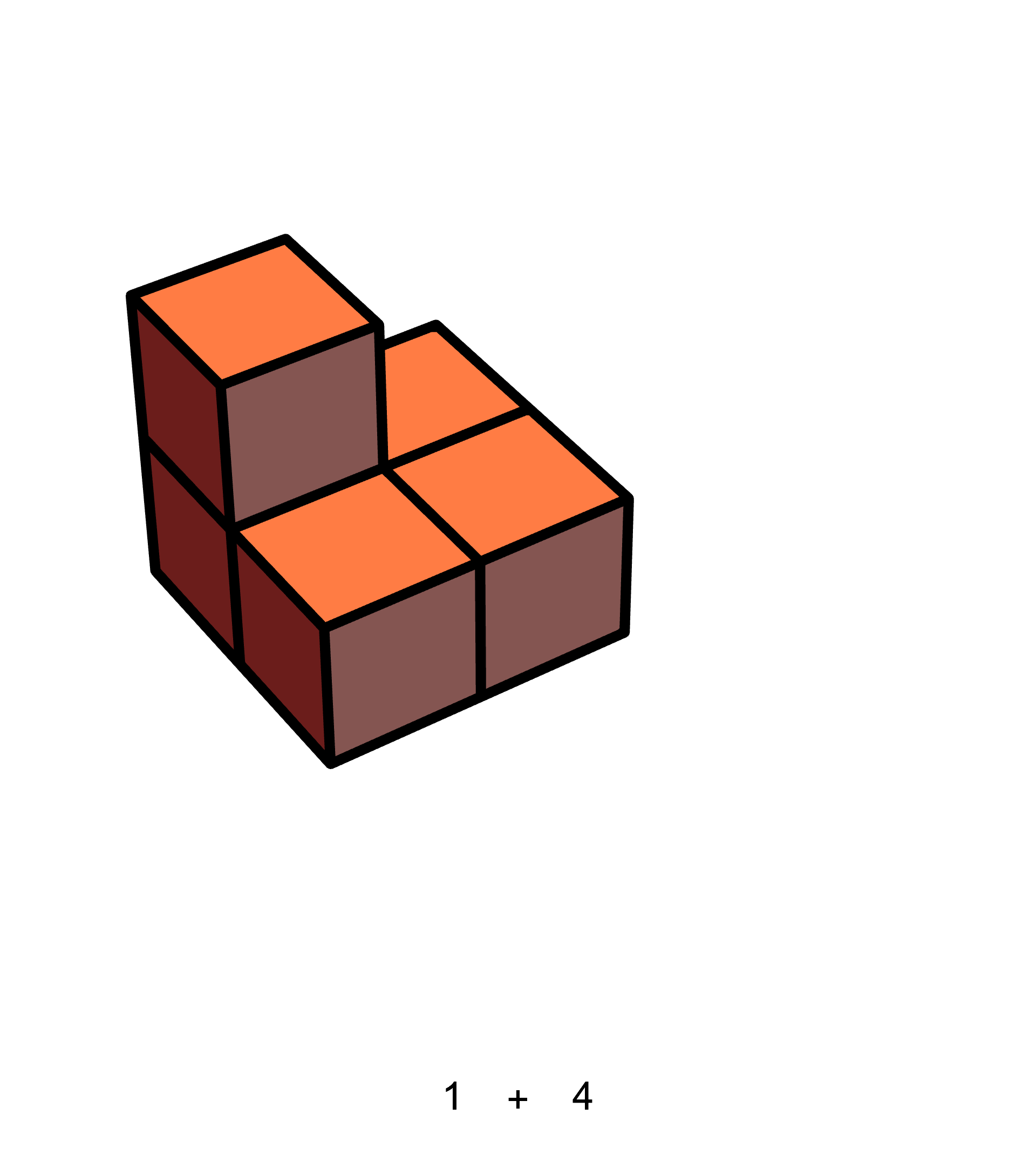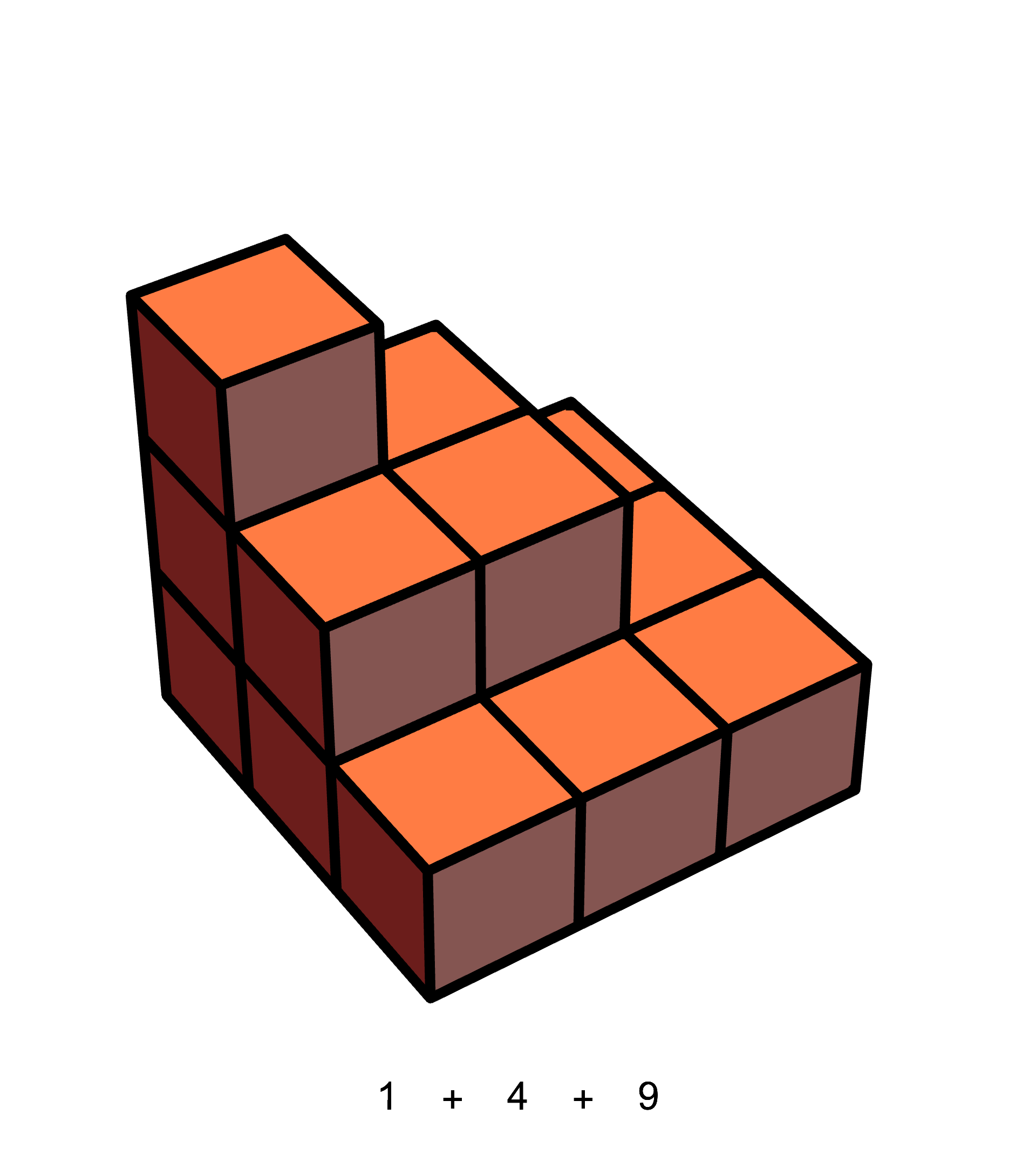
And then observe that 6 of these staircases can be assembled into a cuboid:
So,
I'm still curious about whether or not a similar construction exists for sums of