Smoothed Constructive Solid Geometry
Many complex shapes can be described as combinations (e.g. unions, intersections, ... ) of simpler shapes. For example, say we have two overlapping capsule shapes:

and we'd like to find a representation of the union of those shapes. One way to characterize the union of two shapes,
where

In https://iquilezles.org/articles/smin/, there are many examples of applications where defining the geometry using "smooth" boolean operations is preferable. Luckily, this can be accomplished by making a small change to our region definition, to use a smooth minimum instead of the "hard" minimum
Although there are many different smooth min functions, in this document we'll assume smin refers to the "exponential smooth min" described in the linked document above.
Then, the resulting geometry includes fillet-like features (where the radius is controllable by a parameter) where the primitive shapes are close to each other.
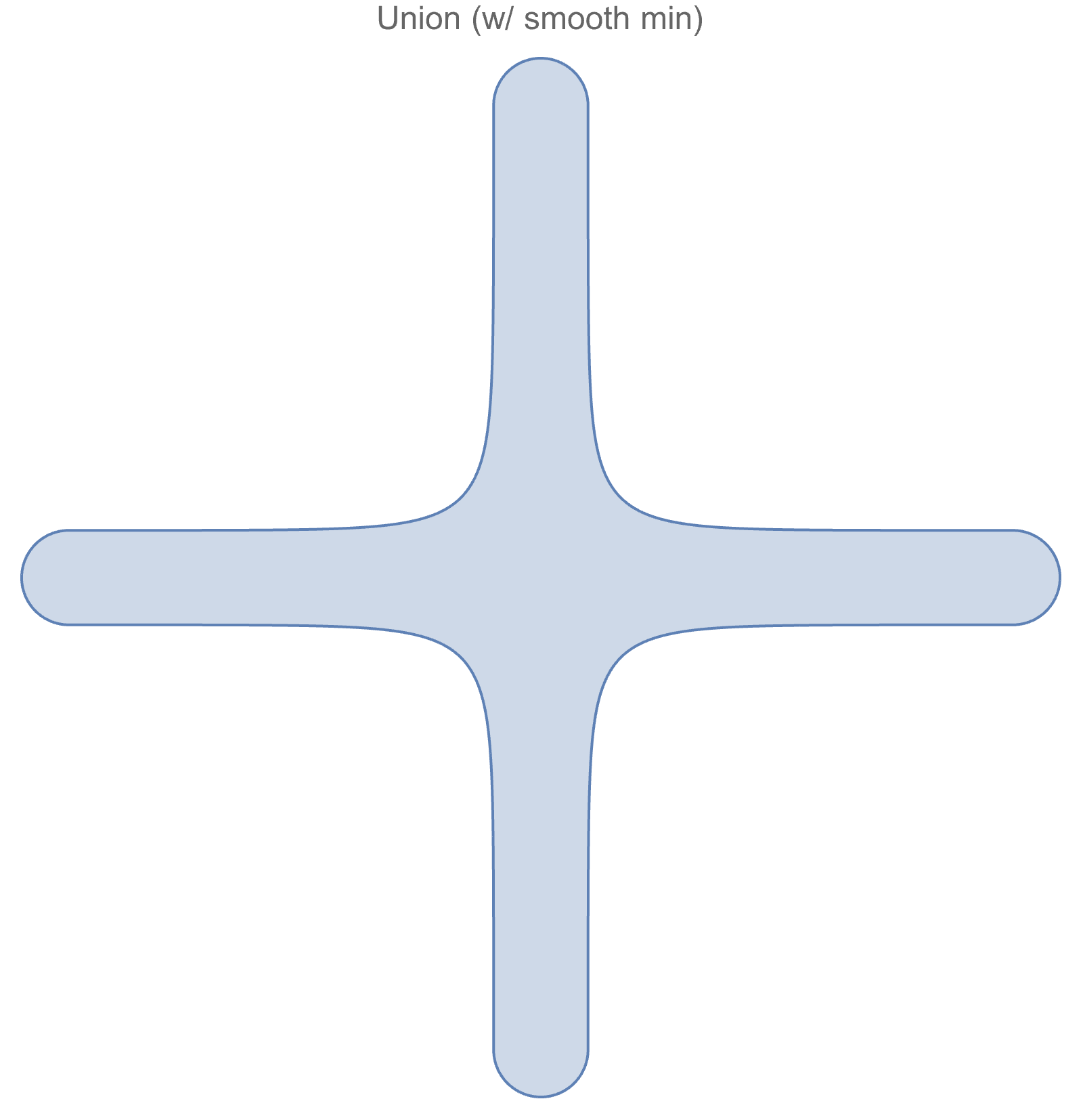
While this process works well for the simple example above, there are some important cases where naively joining primitives by smoothed operations can result in undesirable geometry.
Problems with Overlapping Endpoints
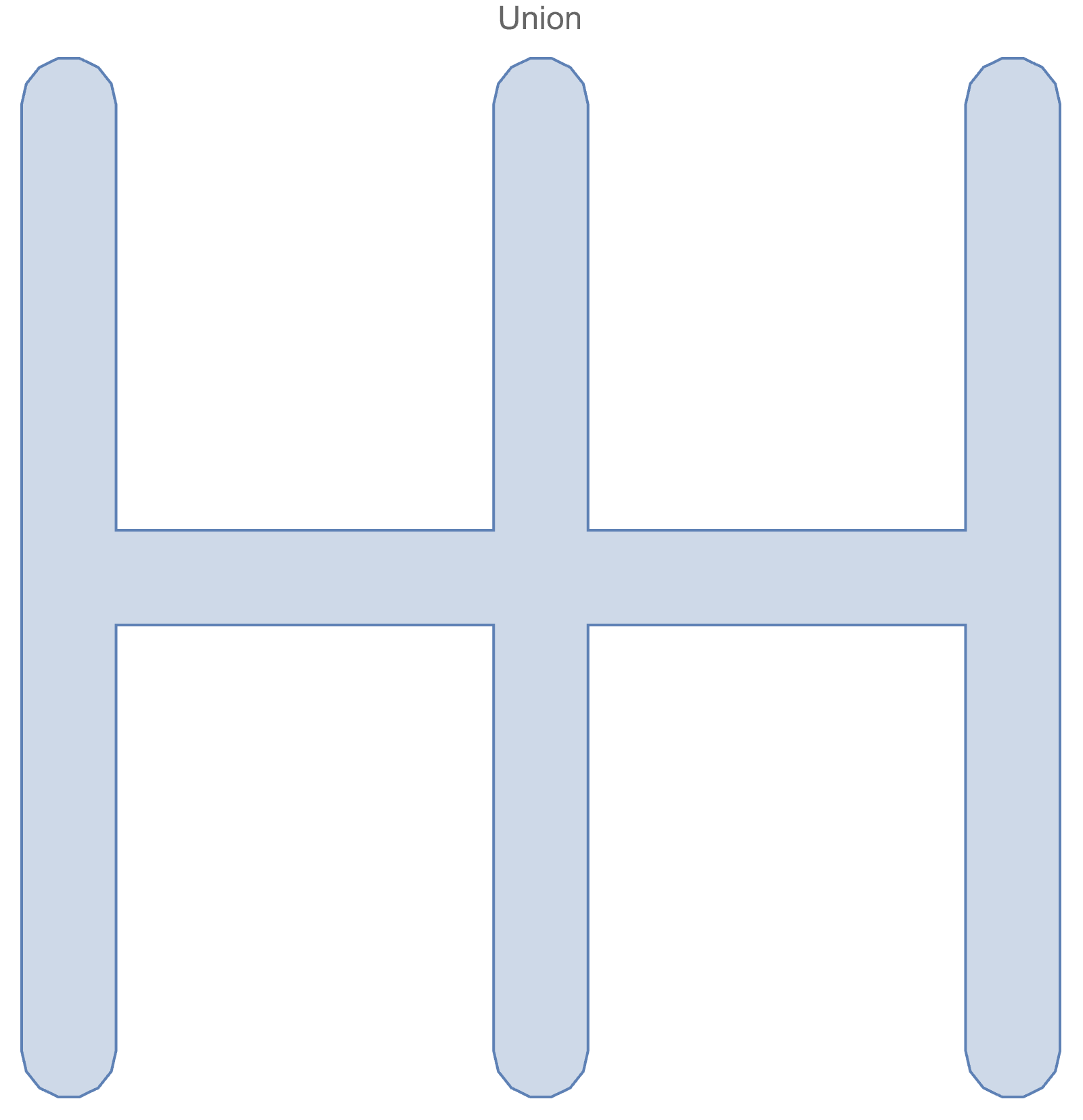
Now, let's consider a slightly more interesting example with 6 capsule shapes

the implicit region defined by the "hard" minimum gives us the union shape we expect
But, what if we wanted a geometry with rounded fillets instead of sharp corners where the primitives intersect? In the first example, we showed that can be accomplished by using a smooth minimum, let's give that a try
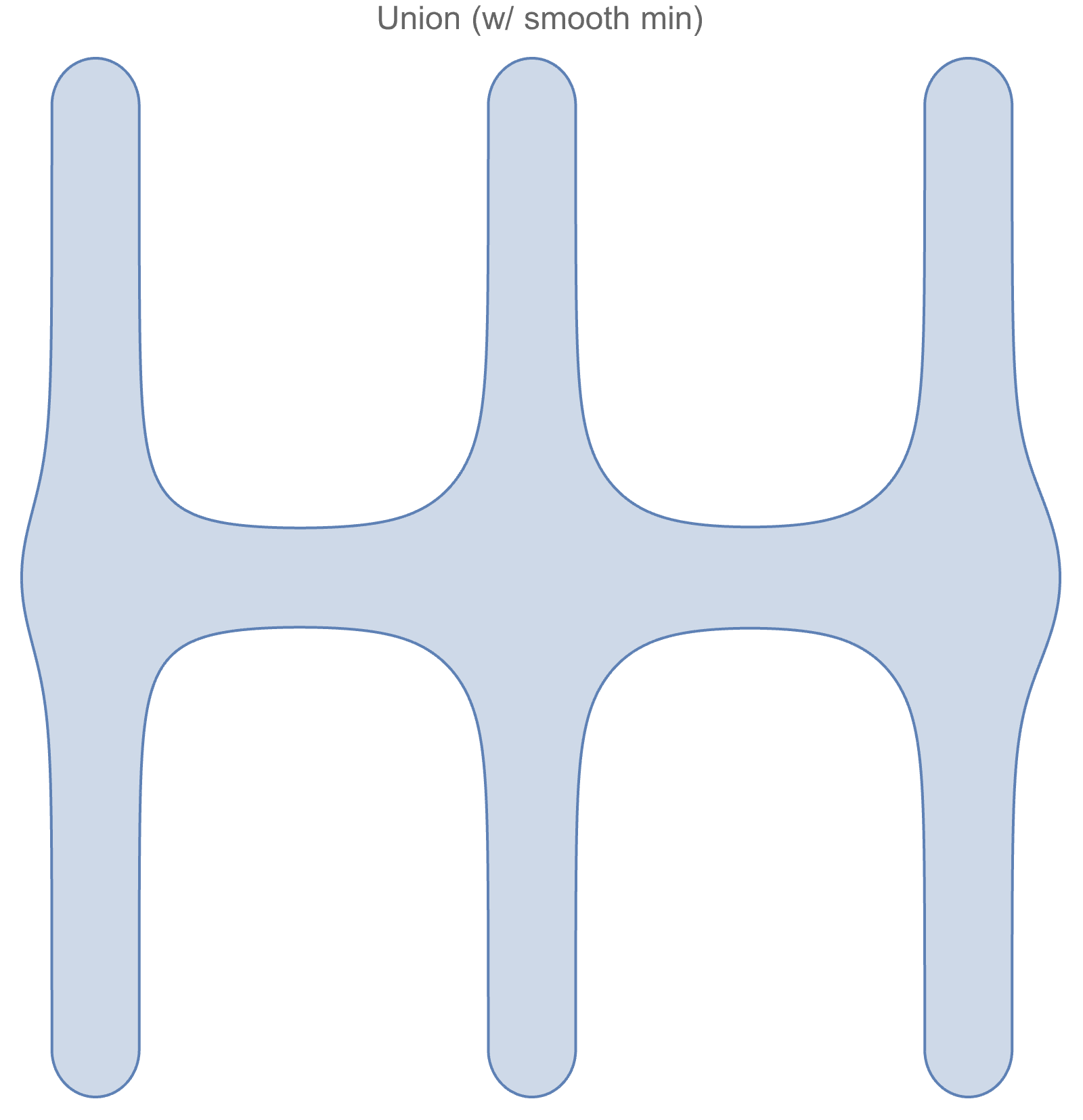
Well, it certainly has the fillets at the intersections, but it also has (probably undesirable) bulbous features too. Additionally, although the region produced by the "hard" minimum has mirror symmetry about the vertical axis, the region defined by the smooth minimum doesn't.
Where did those swollen features come from?
Smooth min functions don't behave exactly like the actual min function. For example the actual min function satisfies
but the smooth min doesn't
This means that, even though the left tip of the horizontal blue cylinder from this example satisfies
The smooth min returns a slightly negative value
The "swelling" on the right side of the region is more pronounced than it is on the left, because there are 3 coincident shapes on the right, so there's a larger discrepancy between the smooth min and actual min.
A Potential Fix
So, what can we do about it?
The problem is related to the counterintuitive property of the smooth min function described above
However, the smooth min does still satisfy
So, the idea behind the fix is to redefine the smooth min function to accept two kinds of arguments:
where
With this in mind, we can now preprocess the geometry and look for places where the endpoints might be counted too many times:
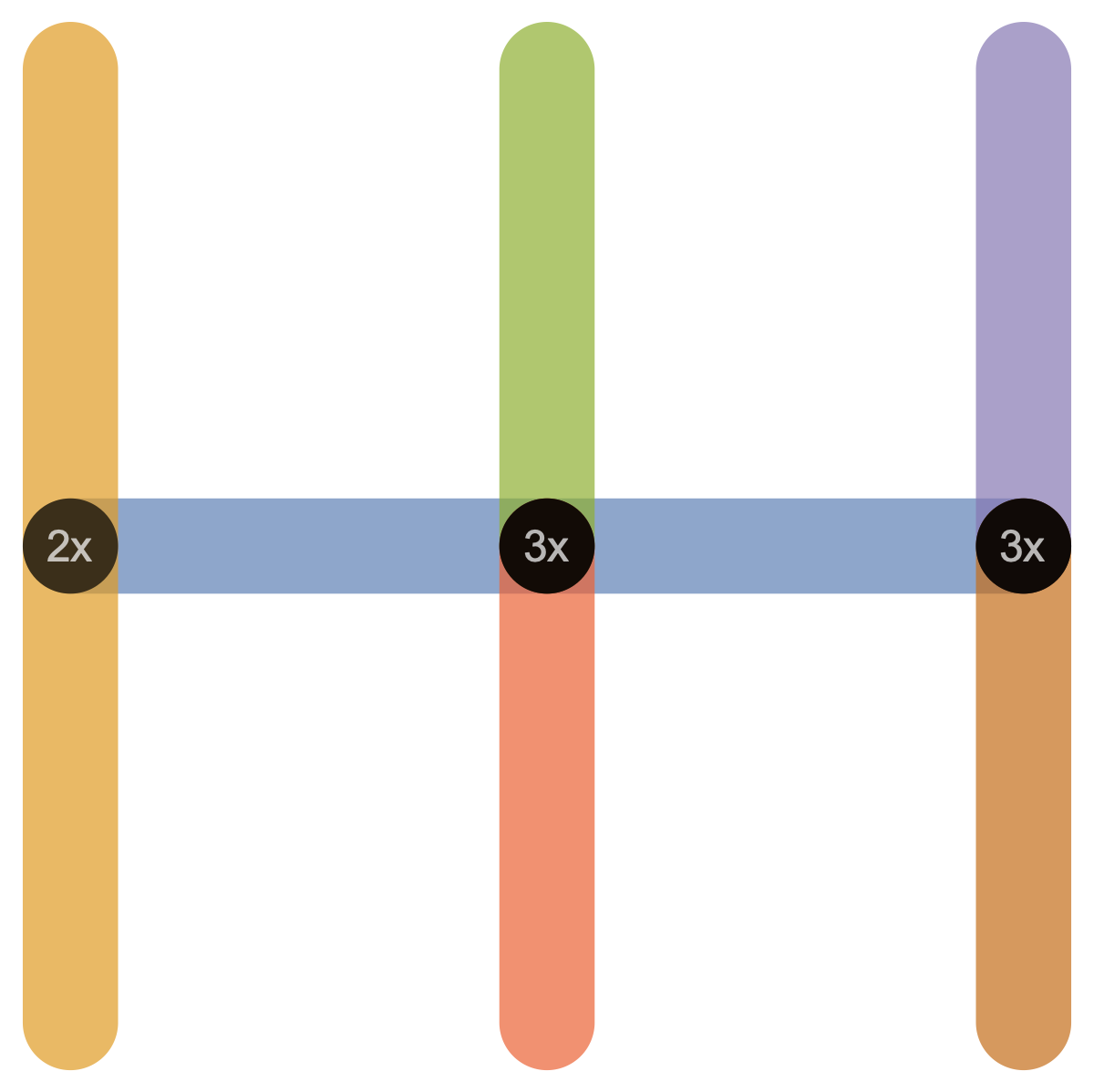
From left to right, the dark circular regions are effectively counted 2x, 3x, and 3x, instead of once. But now that we have the ability to negate contributions in the smin calculation, we can go back and add in spherical SDF contributions with weights -1x, -2x, and -2x to bring the multiplicity for those regions back to 1.
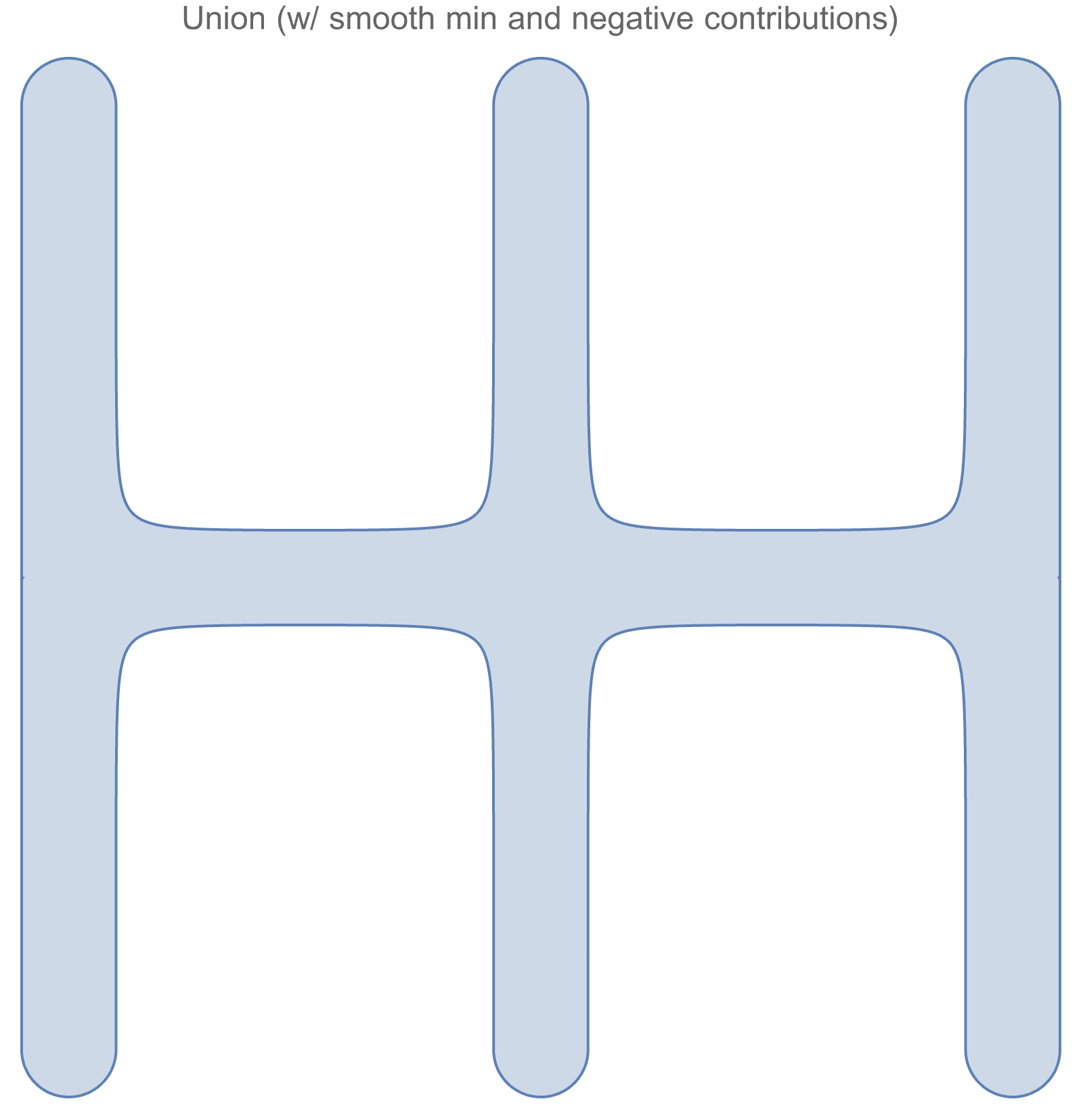
This geometry looks much better than the initial smooth min version, but it still has a few notable downsides over using the true minimum:
The exponential function is more expensive to evaluate.
The exponential smooth min hurts the locality of the calculation. This means that to calculate the smooth SDF of at a point, one needs to evaluate SDFs to all shapes within a distance of
It requires some additional preprocessing to identify overlapping endpoints and their multiplicity.
It slightly dilates the geometry everywhere.