Regular Newmark-$\beta$$\beta$ Method

The update procedure of the Newmark-$\beta$$\beta$ method is:

where the accelerations are given by solving $M\ddot{u}+C\dot{u}+f(u)=0$$M \ddot{u} + C \dot{u} + f(u) = 0$. For a single-dof toy problem where $f(u)=ku$$f(u) = k \; u$ and there is no damping, then we just have $\ddot{u}=-\frac{k}{m}u=-{\omega }^{2}u$$\ddot{u} = - \frac{k}{m} u = -\omega^2 u$. Plugging this back into the update procedure above gives

Rearrange things so that all the new stuff is on the left, and the old stuff on the right

and put it in matrix form so we can actually see what's going on

If the update matrix $\mathbf{A}$$\bold{A}$ had an eigenvalue with magnitude greater than 1, then applying it over and over would make $u,\dot{u}$$u, \dot{u}$ grow without bound-- which is obviously wrong. So, which combinations of $\{\beta ,\gamma ,\mathrm{\Delta }t\}$$\{\beta, \gamma, \Delta t\}$ ensure that the eigenvalues of $\mathbf{A}$$\bold{A}$ stay inside the unit disk?

Since $\mathbf{A}$$\bold{A}$ is only 2x2, we can just write out its eigenvalues in closed form (with $\tau :=\omega \mathrm{\Delta }t$$\tau \coloneqq \omega \Delta t$):

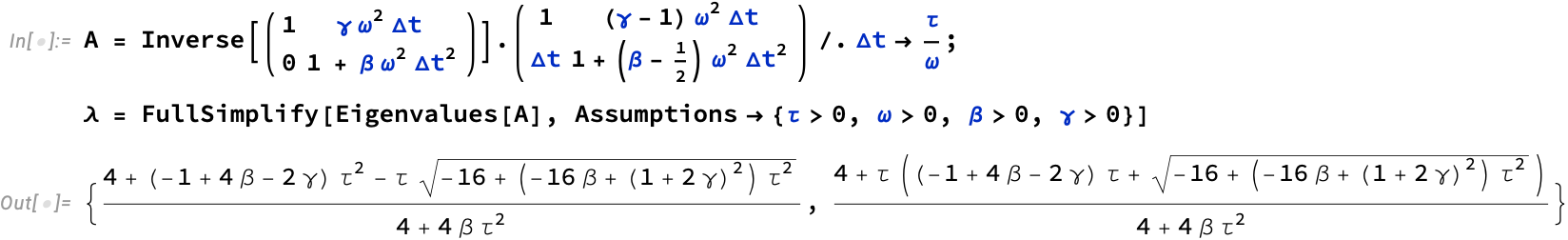
In theory, we could visualize the 3D region defined by $||{\lambda }_{1,2}(\beta ,\gamma ,\tau )||\le 1$$||\lambda_{1,2}(\beta, \gamma, \tau)|| \leq 1$, but instead we'll just fix $\gamma =\frac{1}{2}$$\gamma = \frac{1}{2}$ (since there is no point using Newmark-$\beta$$\beta$ with any other value of $\gamma$$\gamma$) and plot the stability region in 2D:

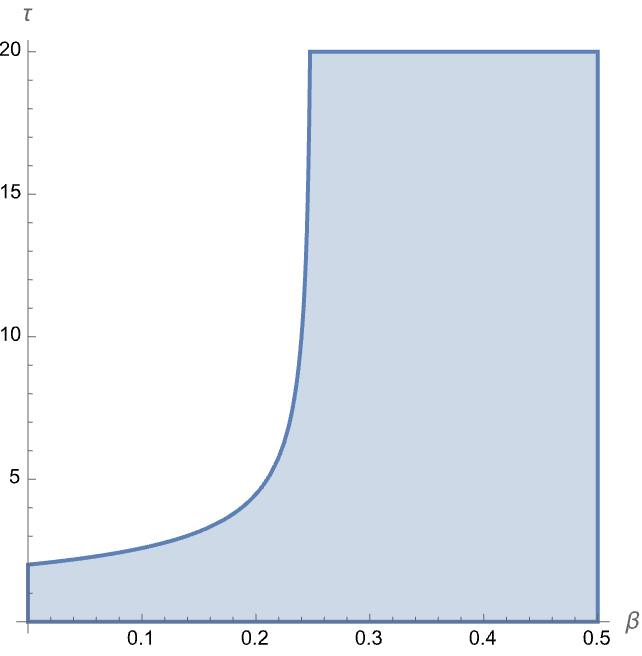
This shows the classical stability results:

• Explicit Newmark ($\beta =0$$\beta = 0$) has a critical timestep defined by $\tau (=\omega \mathrm{\Delta }t)\le 2$$\tau \; (= \omega \Delta t)\leq 2$

• Implicit Newmark with $\beta \ge \frac{1}{4}$$\beta\geq \frac{1}{4}$ is unconditionally stable

Constrained Newmark-$\beta$$\beta$ Method

What happens if we're using Newmark-$\beta$$\beta$ to integrate through time, but we would also like to prescribe the motion of a degree of freedom to match some function of time, $U(t)$$U(t)$?

Displacement Control

One natural way to constrain the motion of that degree of freedom is to modify the way the acceleration is calculated to ensure that the displacement takes on the right value at the end of the step:

This, together with the velocity update step, give us two equations relating $\{{\ddot{u}}_{i+1},{\dot{u}}_{i+1}\}$$\{\ddot{u}_{i+1}, \dot{u}_{i+1}\}$ to $\{{\ddot{u}}_i,{\dot{u}}_i\}$$\{\ddot{u}_{i}, \dot{u}_{i}\}$, so we can figure out the update matrix for this case as well:

Like before, calculate the eigenvalues to figure out the stability criteria

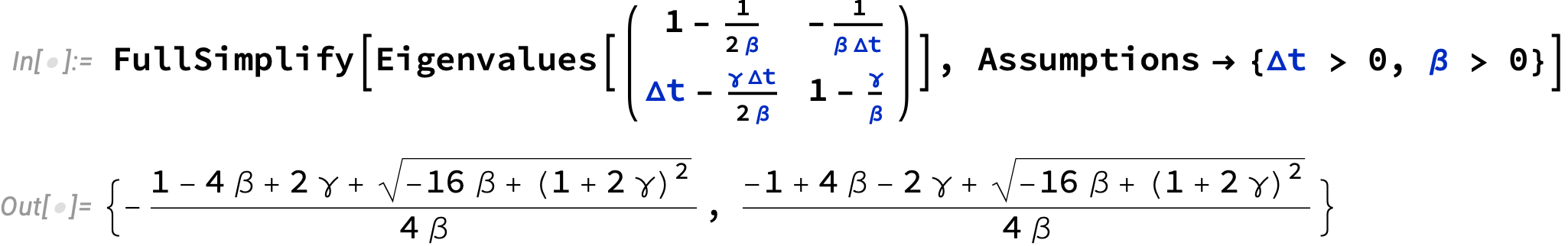
Note: this eigenvalues of this update matrix do not depend on $\mathrm{\Delta }t$$\Delta t$, so any instabilities associated with this enforcement approach do not go away with timestep refinement!

and plot the stability region

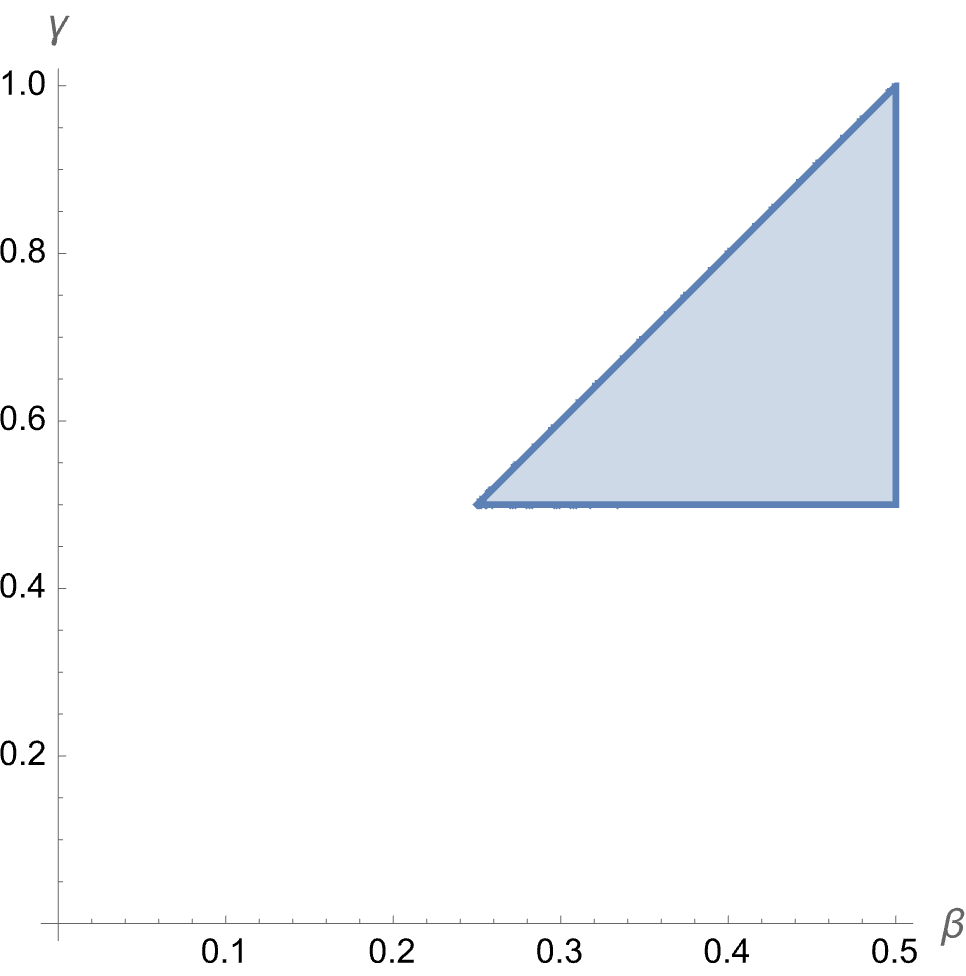
This region is equivalent to the inequality

which is a well-known sufficient condition for Newmark-$\beta$$\beta$ stability, but there is an important difference in this context: it's not a sufficient condition any more, it's a necessary condition. This means that some of the common choices of $\beta =\frac{1}{6}$$\beta = \frac{1}{6}$ (linear acceleration) and $\beta =0$$\beta = 0$ (central difference) do not work with displacement control, for any timestep.

For example, consider what happens when trying to directly prescribe $U(t)=\frac{1}{4}\sin (2\pi t)$$U(t) = \frac{1}{4} \sin(2 \pi t)$, with $\beta =\frac{1}{6}$$\beta = \frac{1}{6}$.

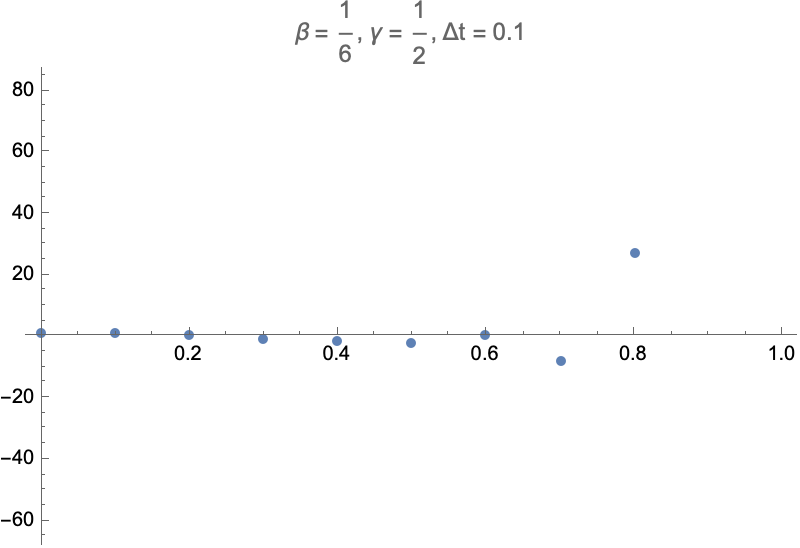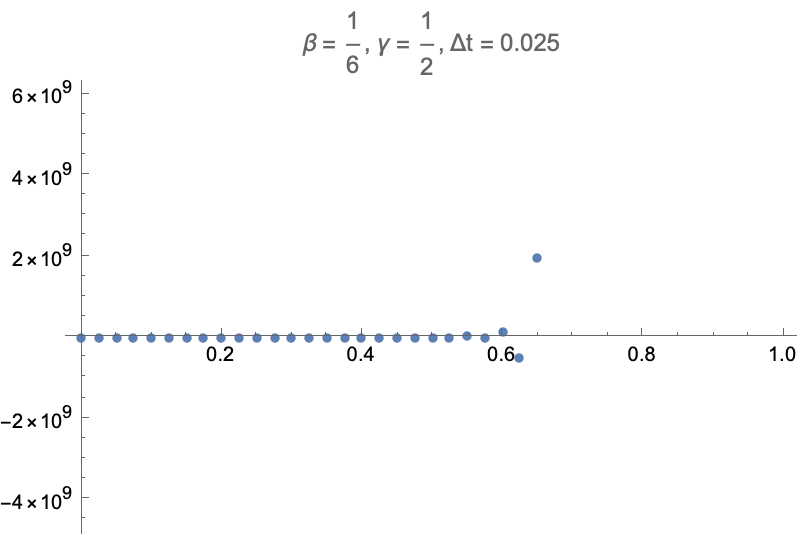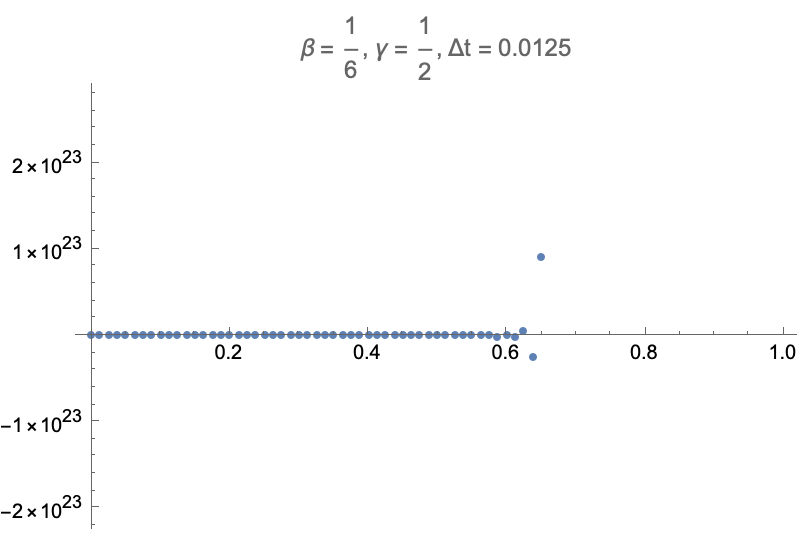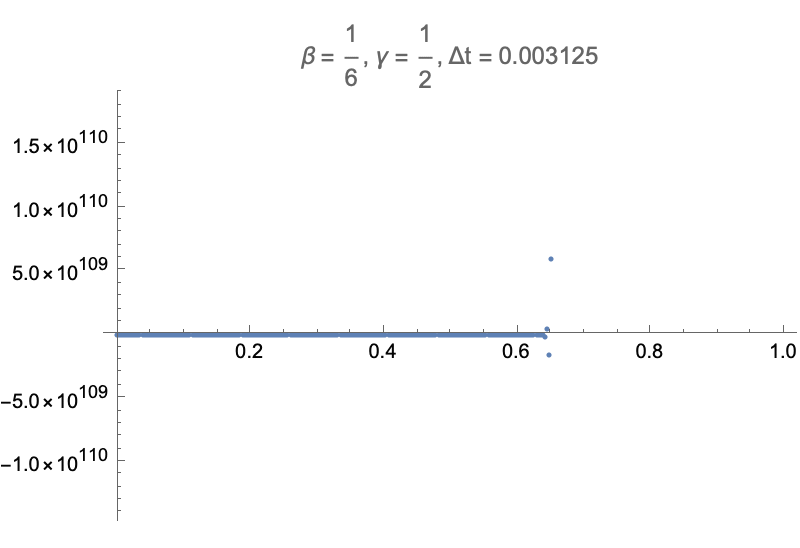
While it's not surprising to see a time integrator go unstable with large timesteps, it is surprising to see that taking arbitrarily small timesteps doesn't help. This goes back to the note earlier about how the stability of the constrained dofs doesn't depend on the timestep. So, displacement control cannot be used with linear acceleration or central difference methods.

Velocity Control

Another possible interpretation of the constraint is ${\dot{u}}_{i+1}=\dot{U}(t_{i+1})$$\dot{u}_{i+1} = \dot{U}(t_{i+1})$. If we put this assumption into the update equations like before and turn the algebraic crank, we eventually get

This time around, the eigenvalues of the update matrix are simple

and the expression for $\lambda$$\lambda$ just tells us that $\gamma \ge \frac{1}{2}$$\gamma \geq \frac{1}{2}$ (which is already satisfied by any of the useful Newmark methods).

Summary

• The stability of "regular" Newmark methods is well known, and rederived here for completeness.

• Prescribing constraints can impose additional stability criteria

  • Constraining displacements directly makes all of the $\beta <\frac{1}{4}$$\beta < \frac{1}{4}$ methods unstable

  • Constraining velocities imposes no additional stability criteria (in practice)

• Although the velocity control approach is preferable for its stability, it also potentially suffers from displacement "drift" over time, since the numerical integration of $\dot{U}(t)$$\dot{U}(t)$ is not exact.

Mathematica notebooks are available for the stability analyses and a basic numerical example.