Multigrid Motivation
Multigrid methods can be an effective way to solve PDEs numerically. Conceptually, the idea behind mulitigrid is to take the original mesh and create coarser and coarser versions of it:
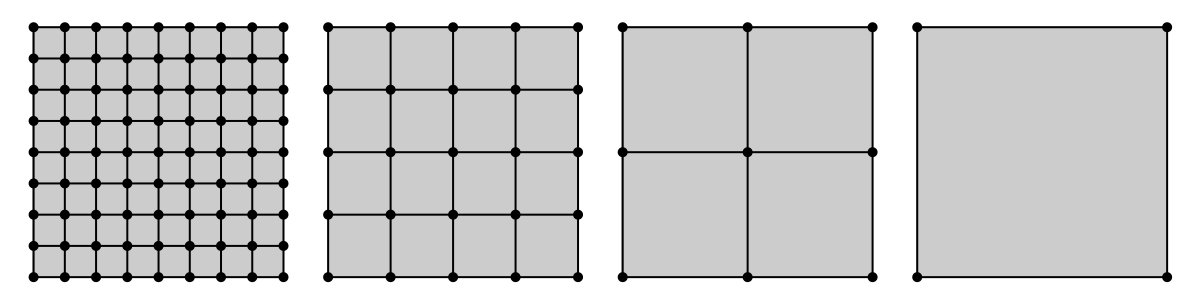
From there, we observe that:
the solutions on the coarser meshes are similar to the solutions on finer meshes
the coarse meshes have significantly fewer degrees of freedom, making them much faster to solve
Together, these ideas let us use the information about solutions from the coarser meshes to improve the solution on the original (fine) mesh. In some cases, a PDE discretized over a mesh of
So, if multigrid is so great, why isn't everyone using it?
Well, one of the big hurdles is with the very first step: creating a sequence of coarsened meshes (once again, meshing proves to be the hardest part of finite element analysis). This step may be trivial when considering structured meshes of rectangular domains, but what do we do if the geometry is more interesting?
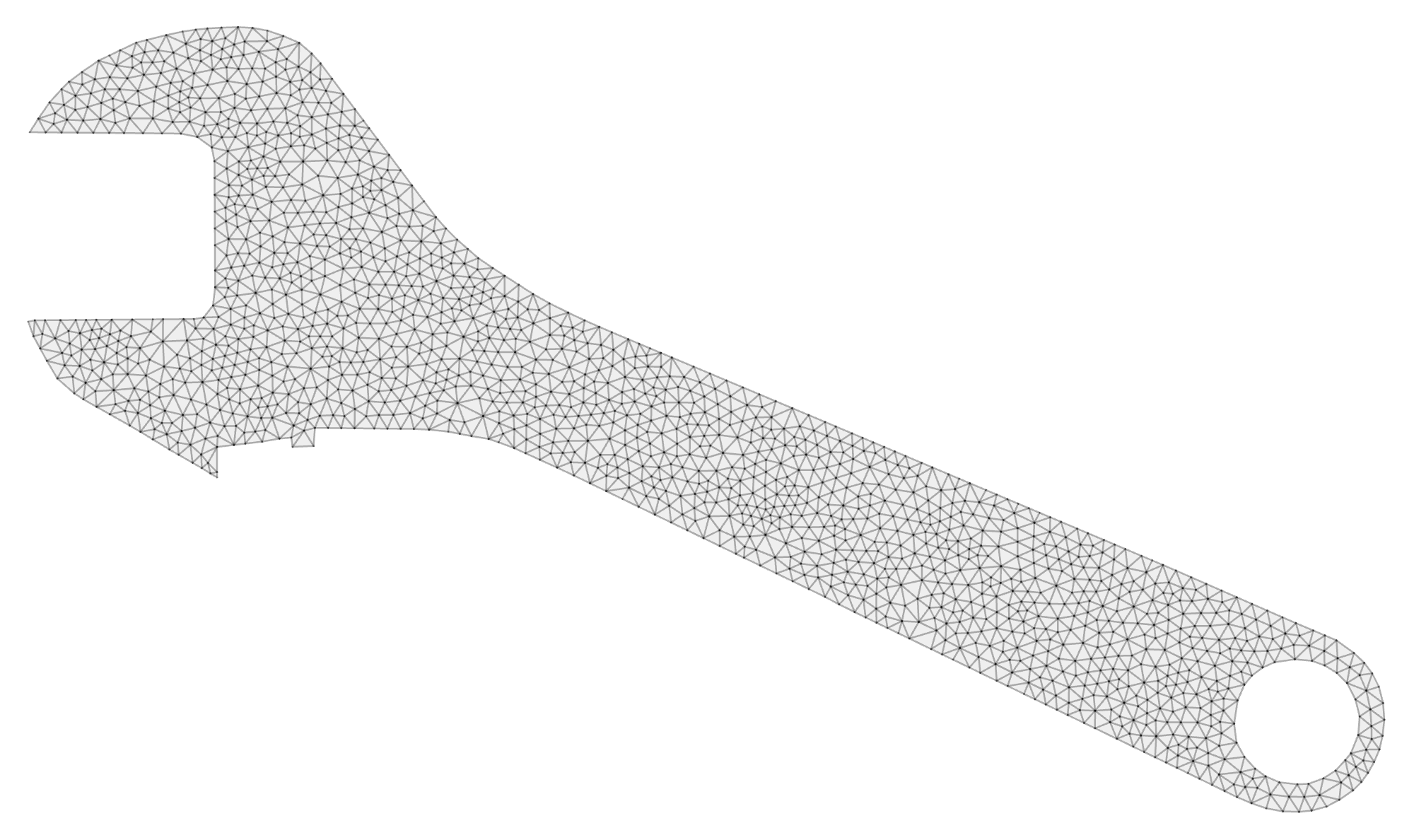
These notes describe an algorithm prototype for repeatedly coarsening simplex meshes.
Unstructured Mesh Coarsening
At the heart of this algorithm is the idea that the coarse meshes in the hierarchy reuse some of the existing nodes/edges from the finer mesh. So: if we can systematically discard some fraction of the nodes and reconnect the remaining ones, then we will have created a coarser mesh.
Graph Coloring
One possible way to decimate nodes from a fine mesh is by thinking of the nodes and edges of that mesh as a graph, and coloring the vertices of that graph. Then, we can choose to discard all vertices except for those with a specific color. Let's give that a shot:
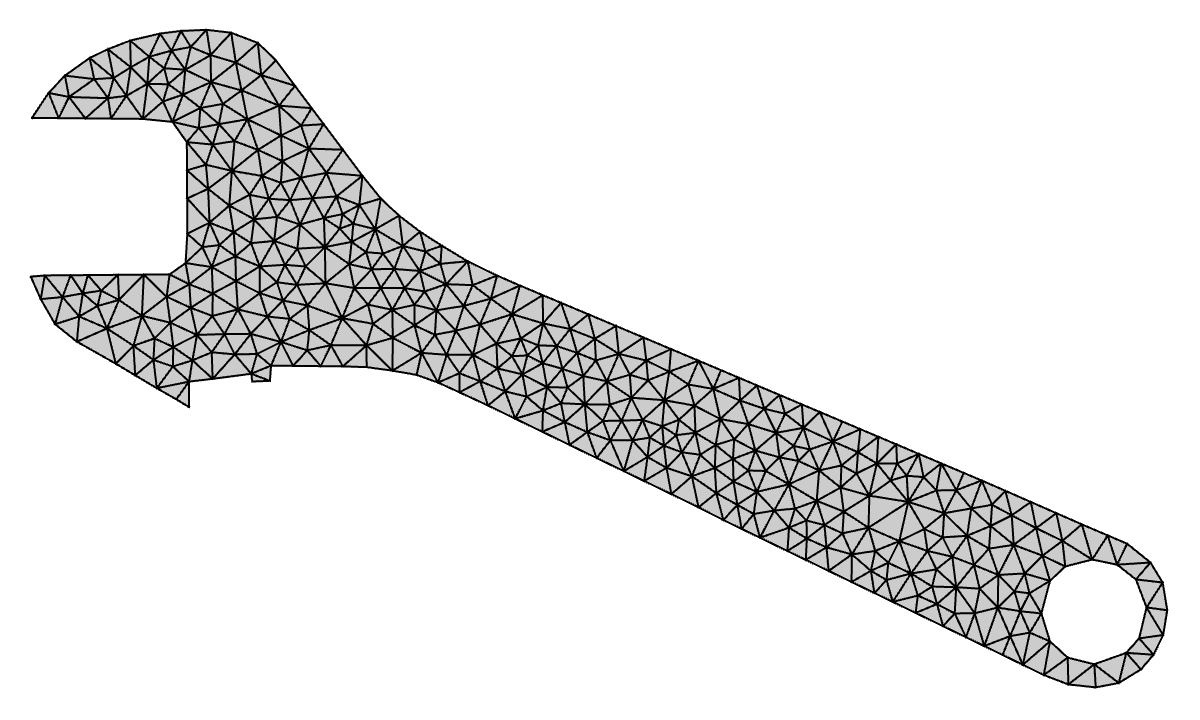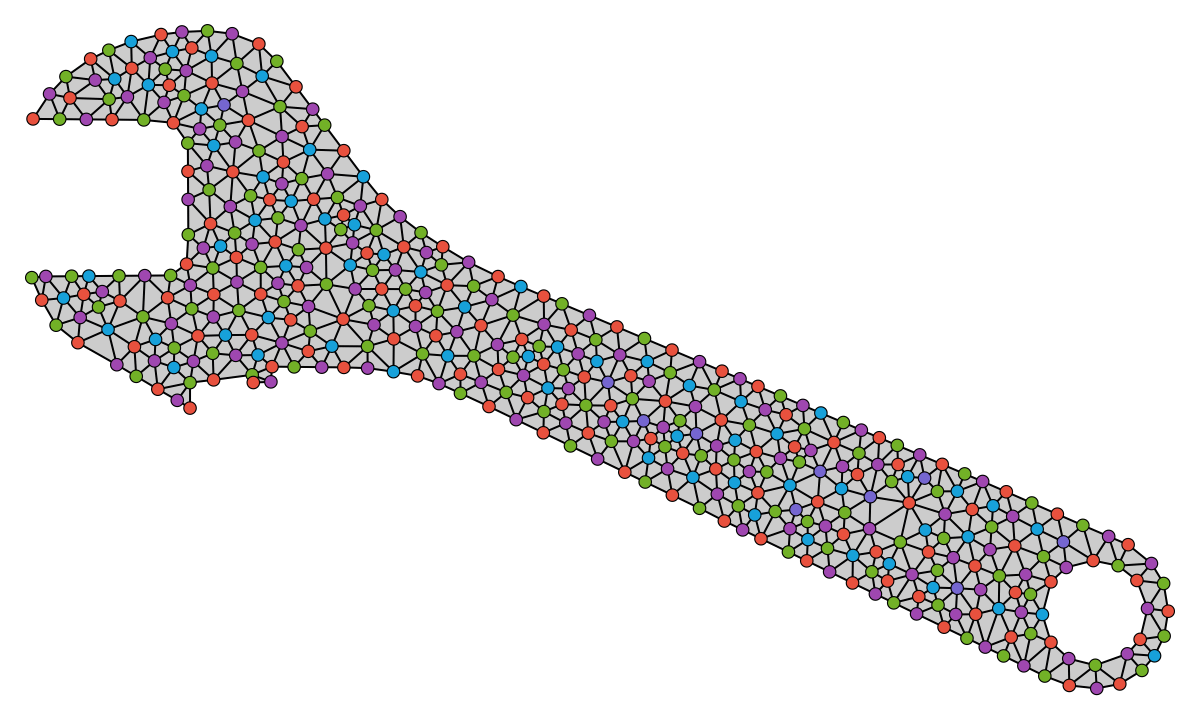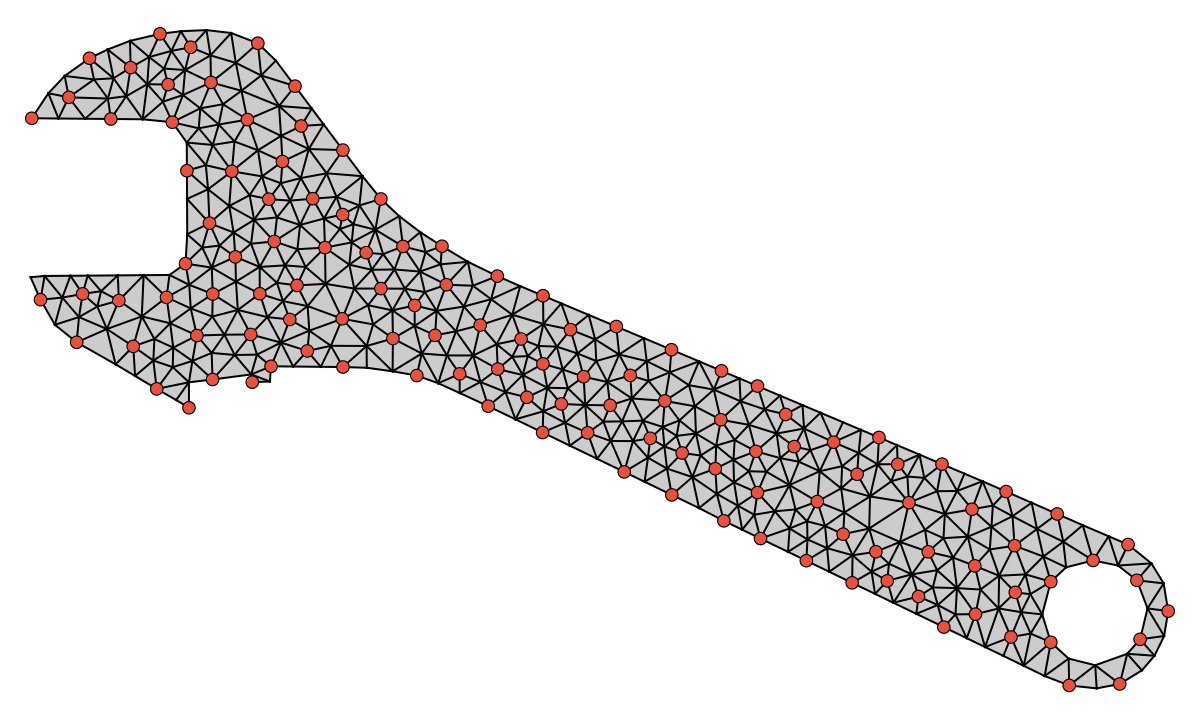
It looks promising so far-- the node coloring algorithm naturally ensures that the coarse nodes are uniformly distributed throughout the mesh, but we still need a way to connect the red nodes to each other. The first approach I tried was to pass the red nodes to an meshing library, and let it perform Delaunay triangulation to reform connections on the coarsened mesh. This approach had a handful of issues, especially with specifying the boundary information to the meshing tool.
Coarse Connectivity
The most unsatisfying part of remeshing the coarse nodes from scratch is that it doesn't make use of the existing connectivity of the fine mesh. Another way to think of the coarsening process is that the discarded nodes don't simply vanish, but instead they merge together with a neighboring red node (which is guaranteed to exist by the graph coloring algorithm). With this in mind, we can merge each discarded node with a red neighbor (e.g. by proximity). By doing this, the coarse mesh will reuse the connectivity from the fine mesh:

Admittedly, the animation above makes the merging process look like a truly terrible idea-- the coarse mesh may have connectivity, but its shape is mangled beyond recognition. However, the distortion is almost entirely caused by the fact that we're not actually respecting the boundary of the mesh when merging nodes. If we change the merging rules so that nodes on the boundary are only allowed to merge with other nodes on the boundary, then the results look like

It still needs work, but the general shape is preserved much better than before.
Some of the nodes on the boundary aren't getting merged though. What's going on there?
It's because there aren't enough red nodes on the boundary. Recall that the node-merging idea required that every eliminated node have at least one red neighbor. When we changed the merging rules on the boundary, we effectively changed the definition of "neighbor" on the boundary to only include other boundary nodes.
Graph Coloring (with Constraints)
We need more red nodes on the boundary, so let's revisit our graph coloring algorithm. Instead of coloring all the mesh vertices at once, we can start by coloring just the boundary nodes. Then, we can keep the red boundary nodes, and proceed to color the rest of the graph normally:
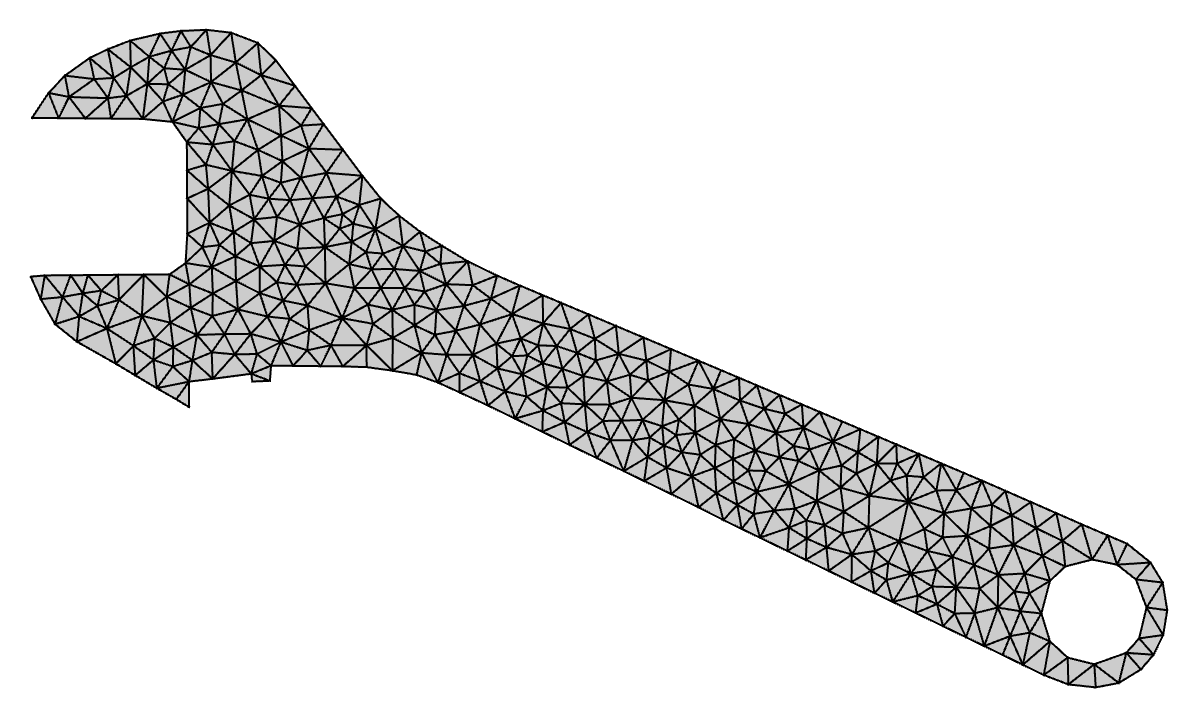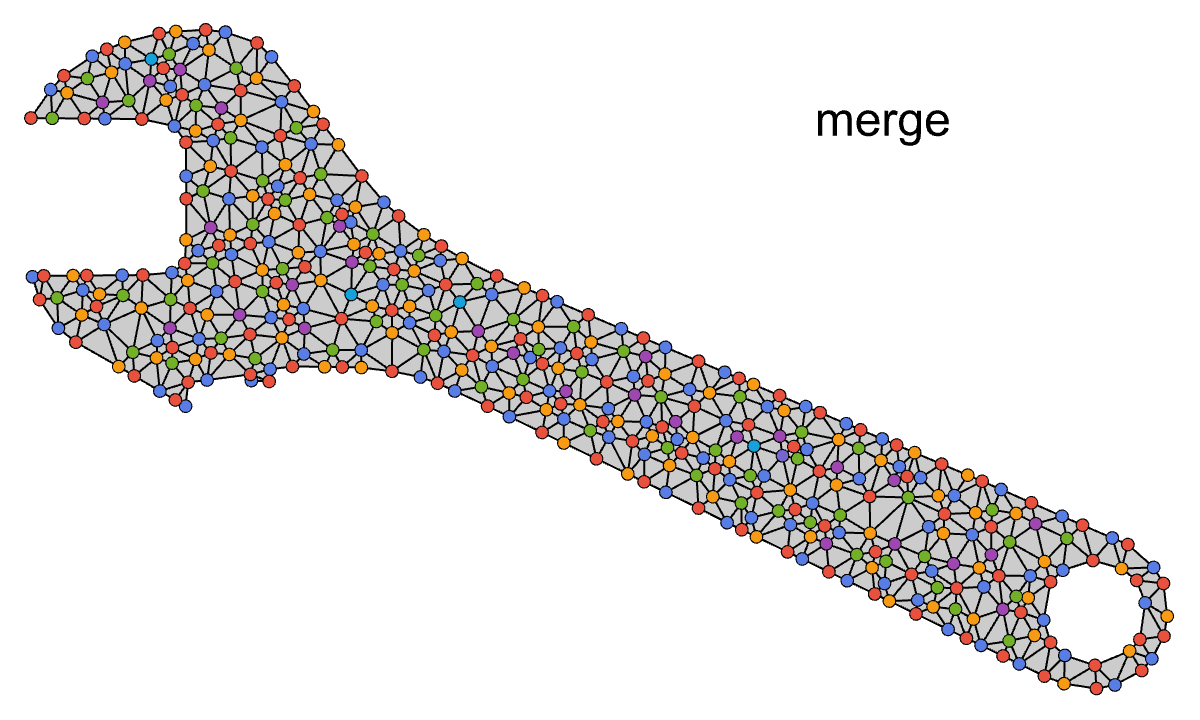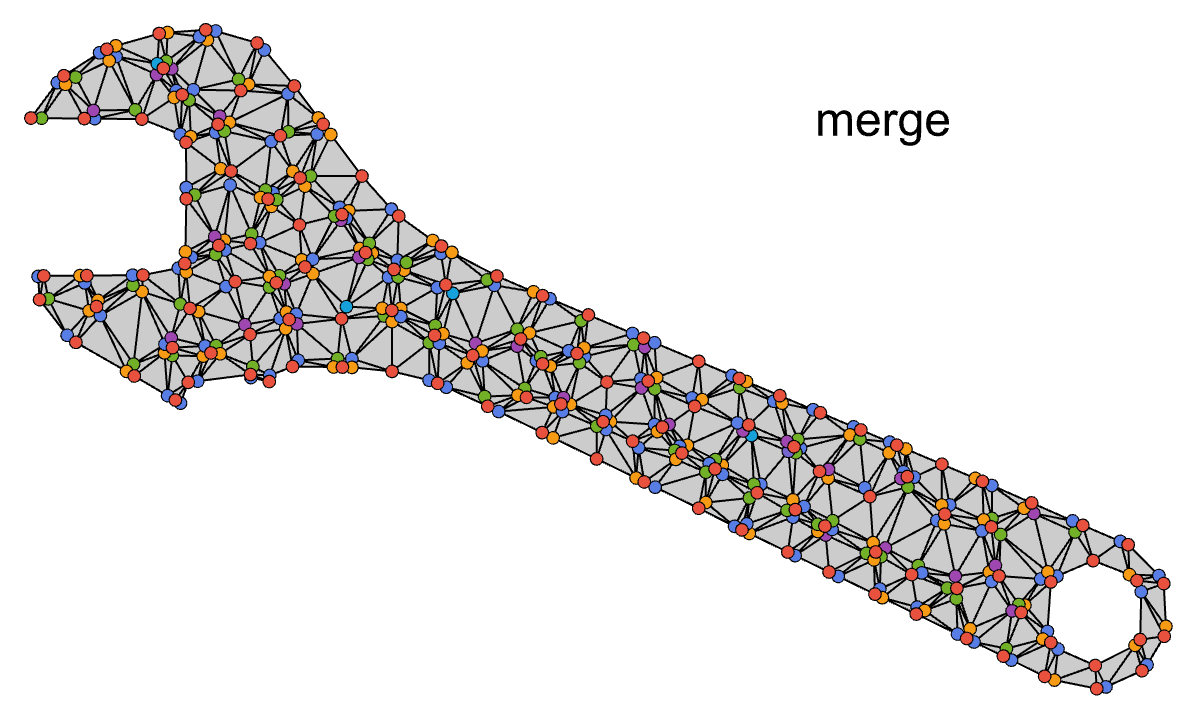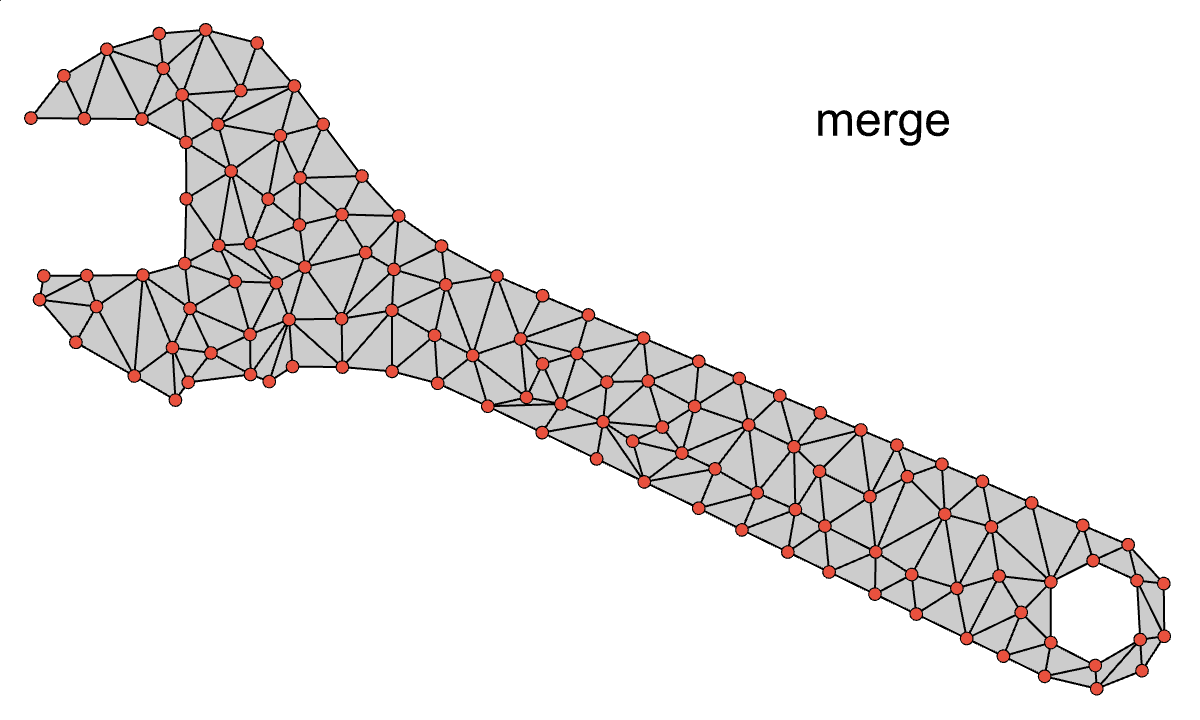
This is looking better, now there are no unmerged nodes on the boundary, but there are still a couple remaining issues:
the sharp corners of the fine mesh aren't preserved in the coarse mesh
the coarse mesh contains some poor quality elements
Preserving corners can be accomplished the same way we preserved the boundary shape: by ensuring that we placed red nodes in the right places. If we start by constraining each sharp corner node to be red, then that feature will be preserved in the coarse mesh. We can detect corners by iterating over nodes on the boundary and finding ones with large curvature.
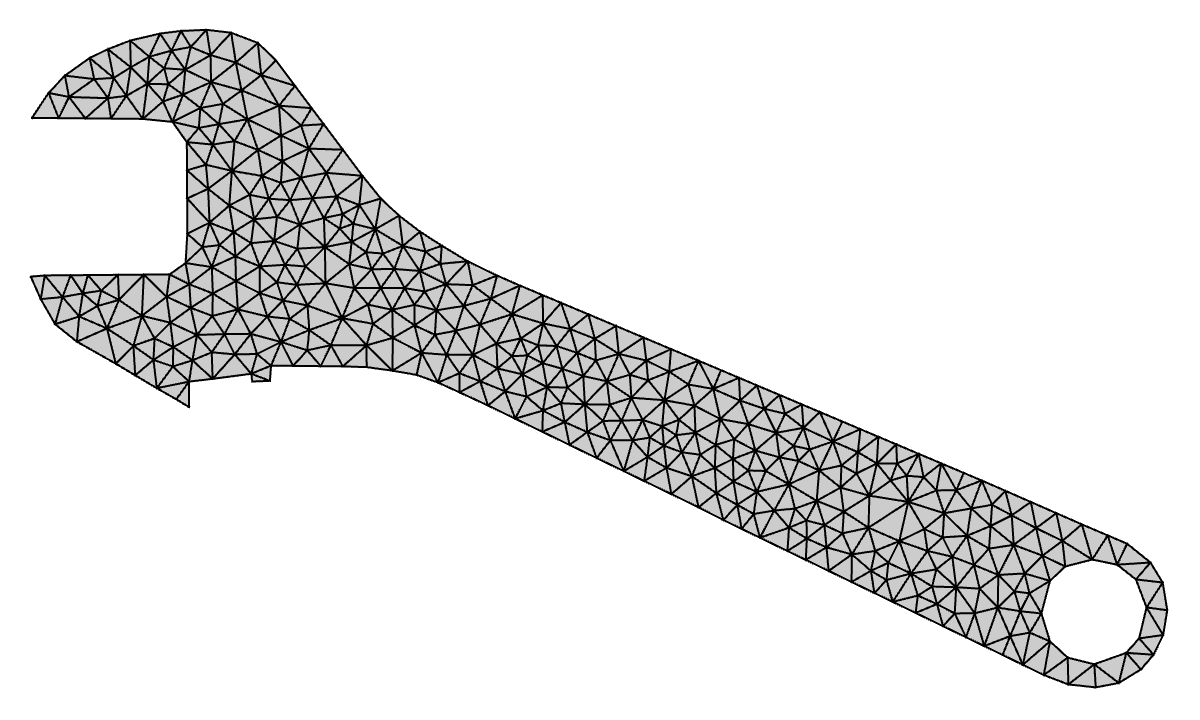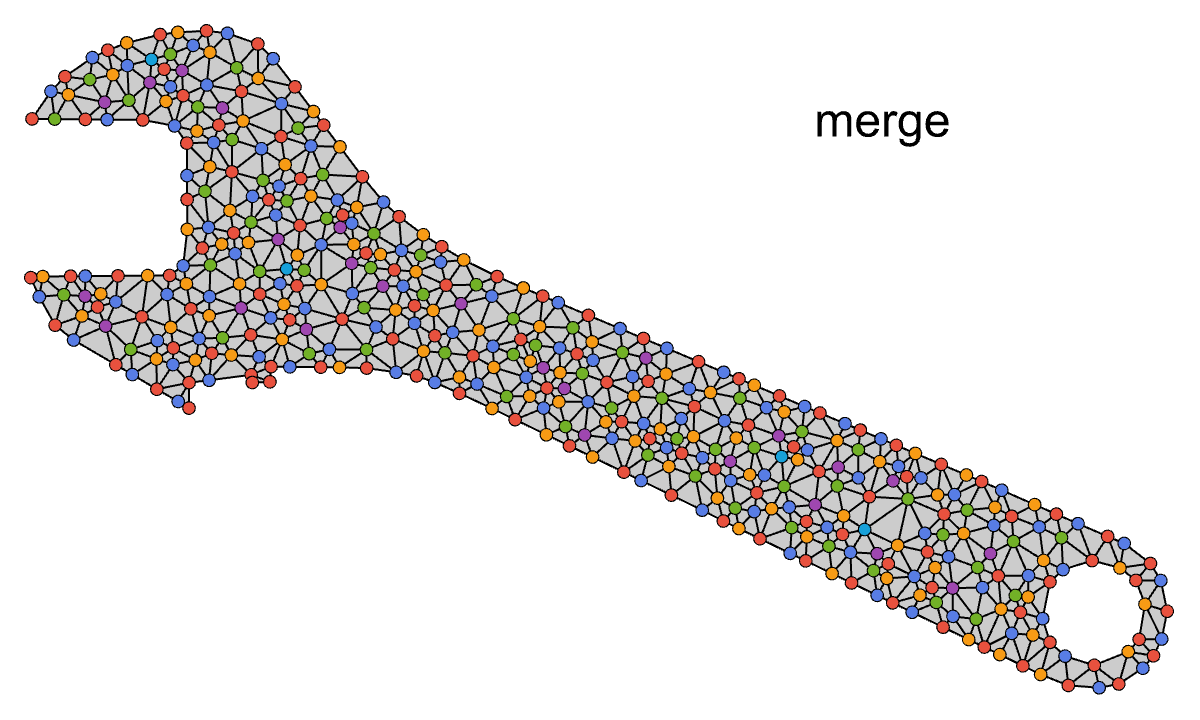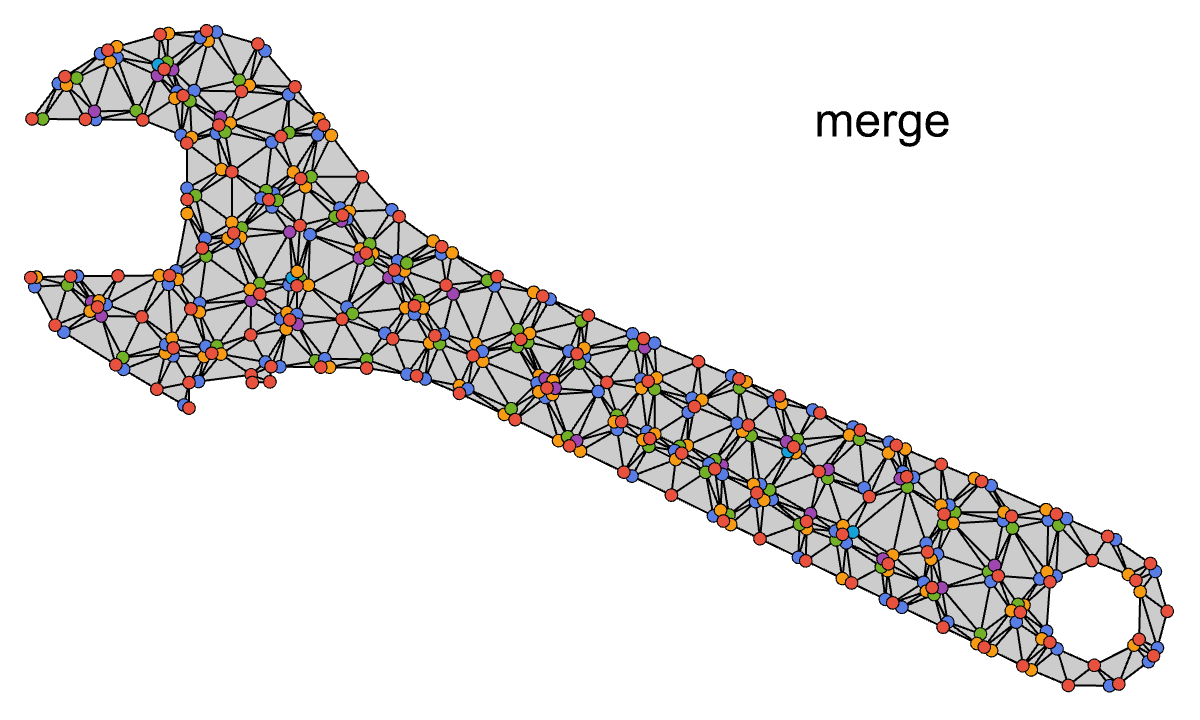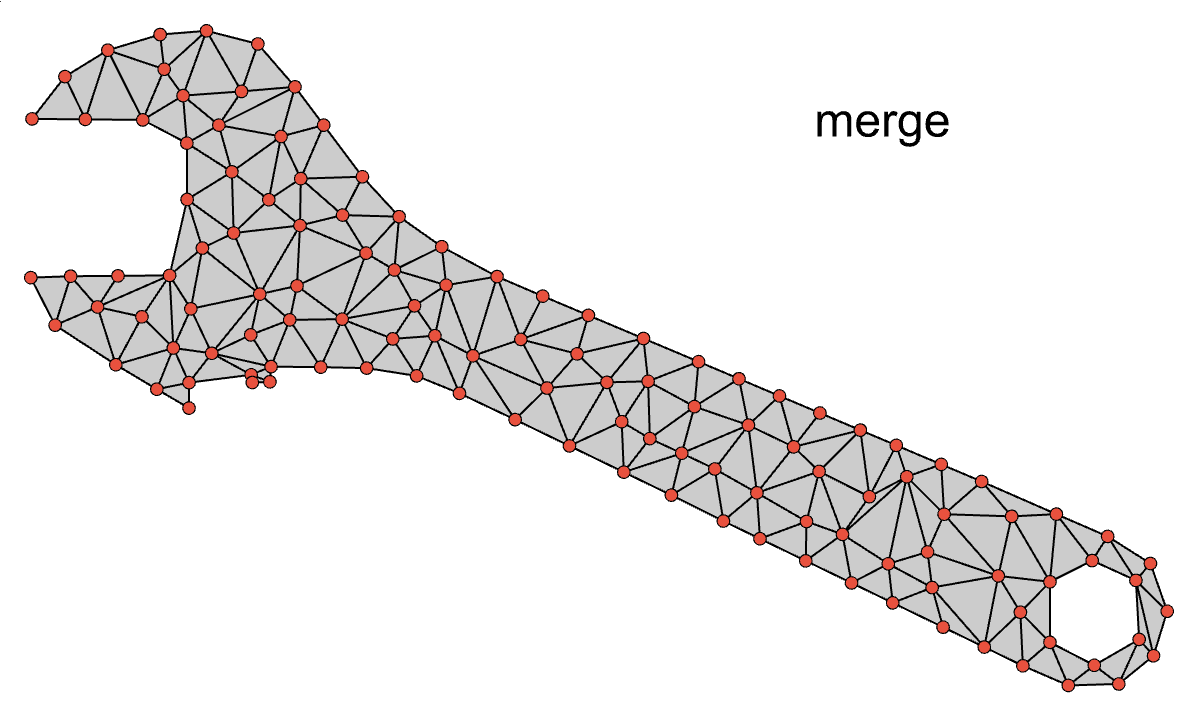
Element Quality
The last piece of the puzzle is how to improve the element qualities in the coarse mesh. I just wrote up a whole article on the subject, so check that out for more details. Conceptually, the idea is to perform gradient ascent on each interior node, maximizing element quality of the surrounding elements. When we apply this iterative procedure to this coarsened mesh we get
Summary
The algorithm's steps are:
Identify corner nodes
Color boundary nodes, respecting corner colors
Color remaining nodes, respecting boundary colors
Merge discarded nodes
Improve coarse mesh element quality by vertex relaxation
There are a few other caveats:
Only works with simplex meshes
Applying the merge step to a fine mesh of quadrilaterals will not result in a coarse mesh of quadrilaterals
Implementation has only been tested in 2D, although each step generalizes to tetrahedron meshes
3D meshes will likely require another step to identify corner edges as well as corner vertices
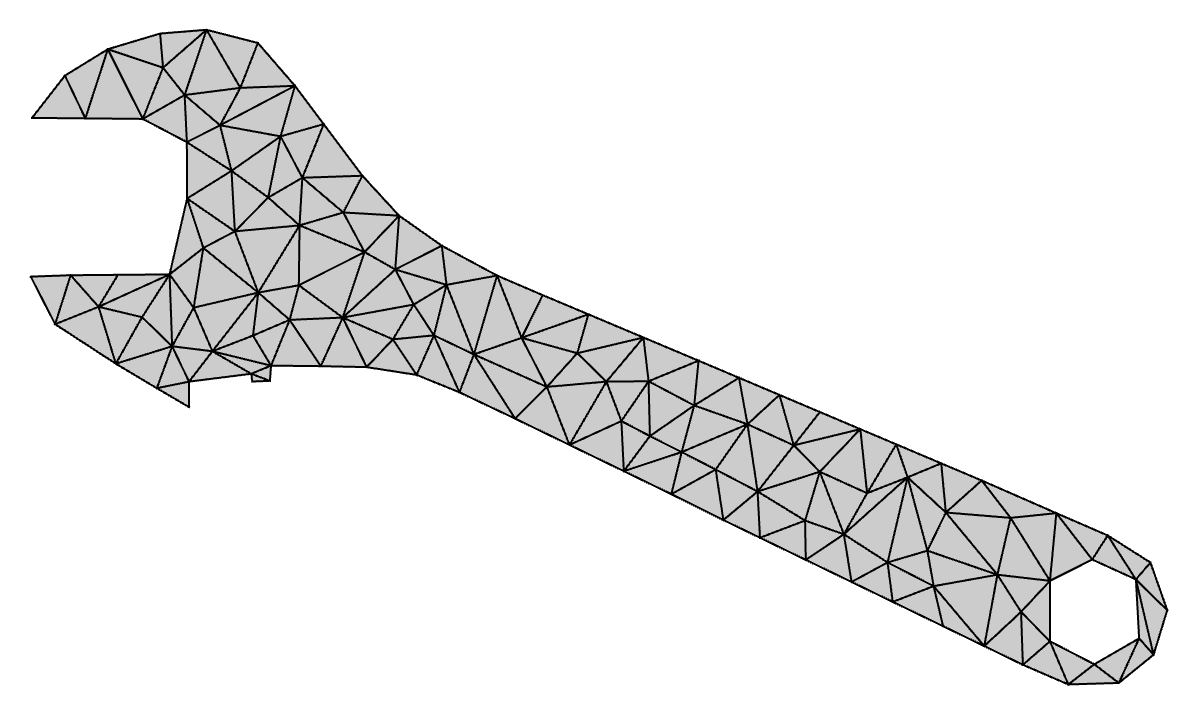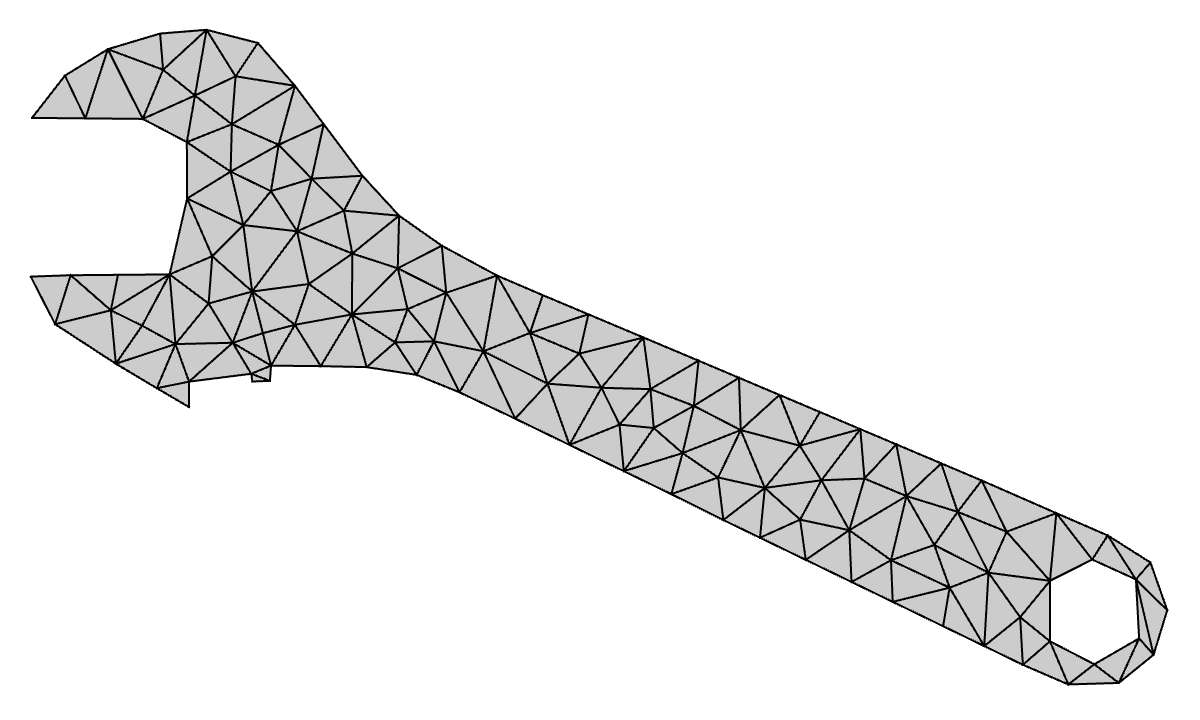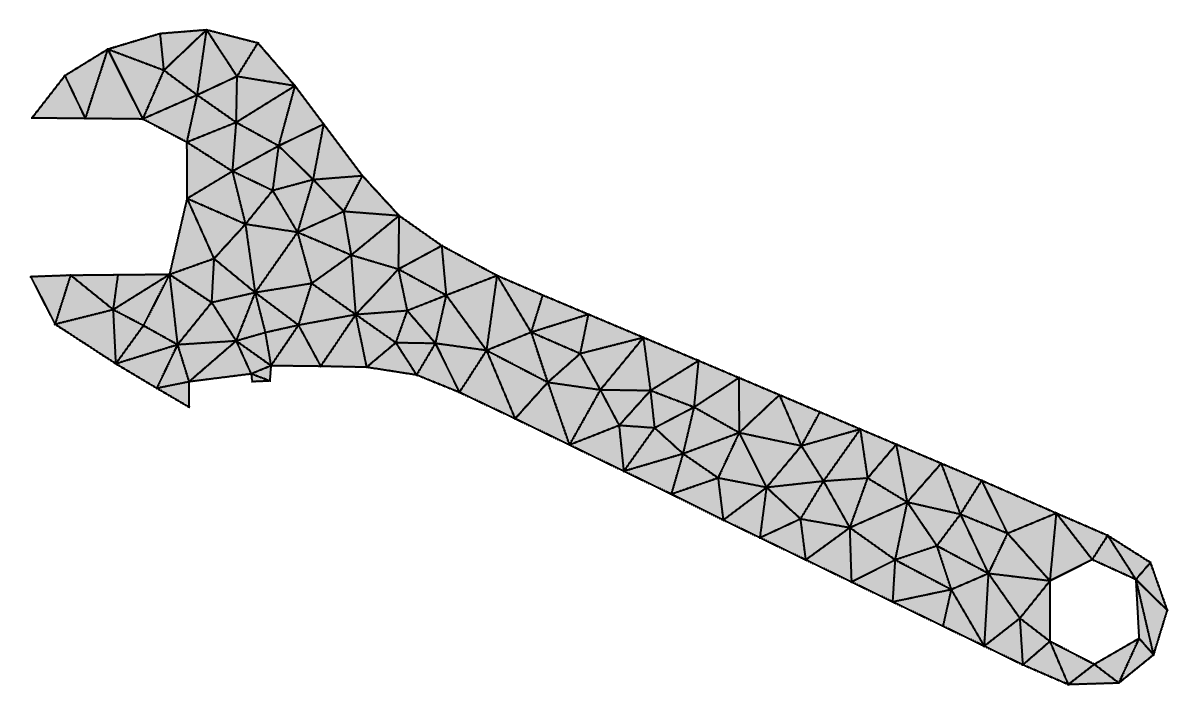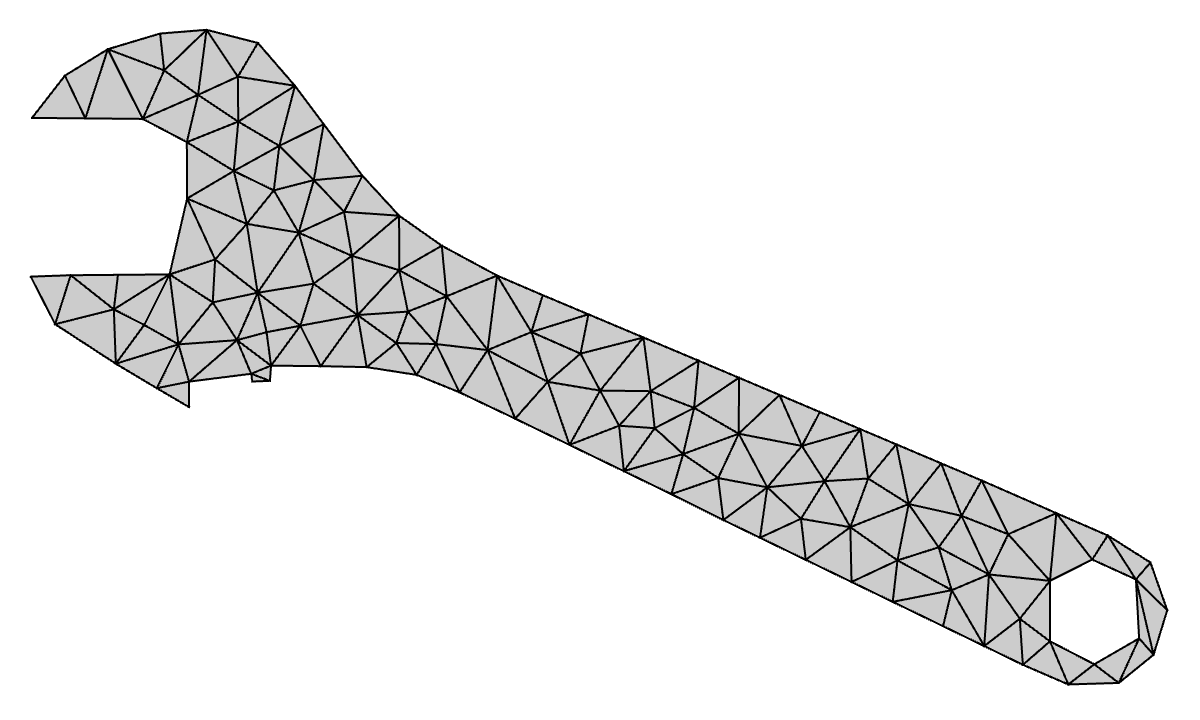
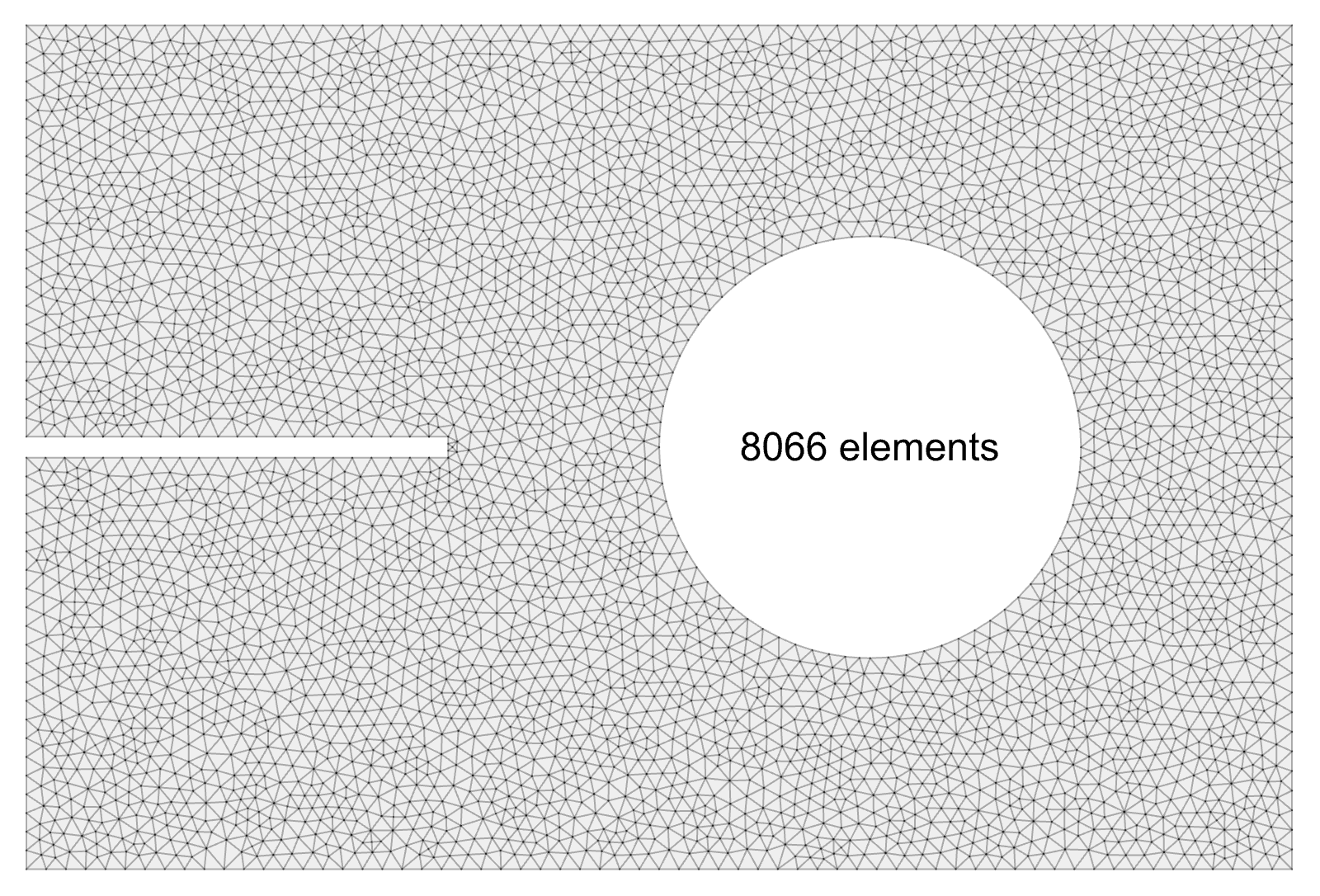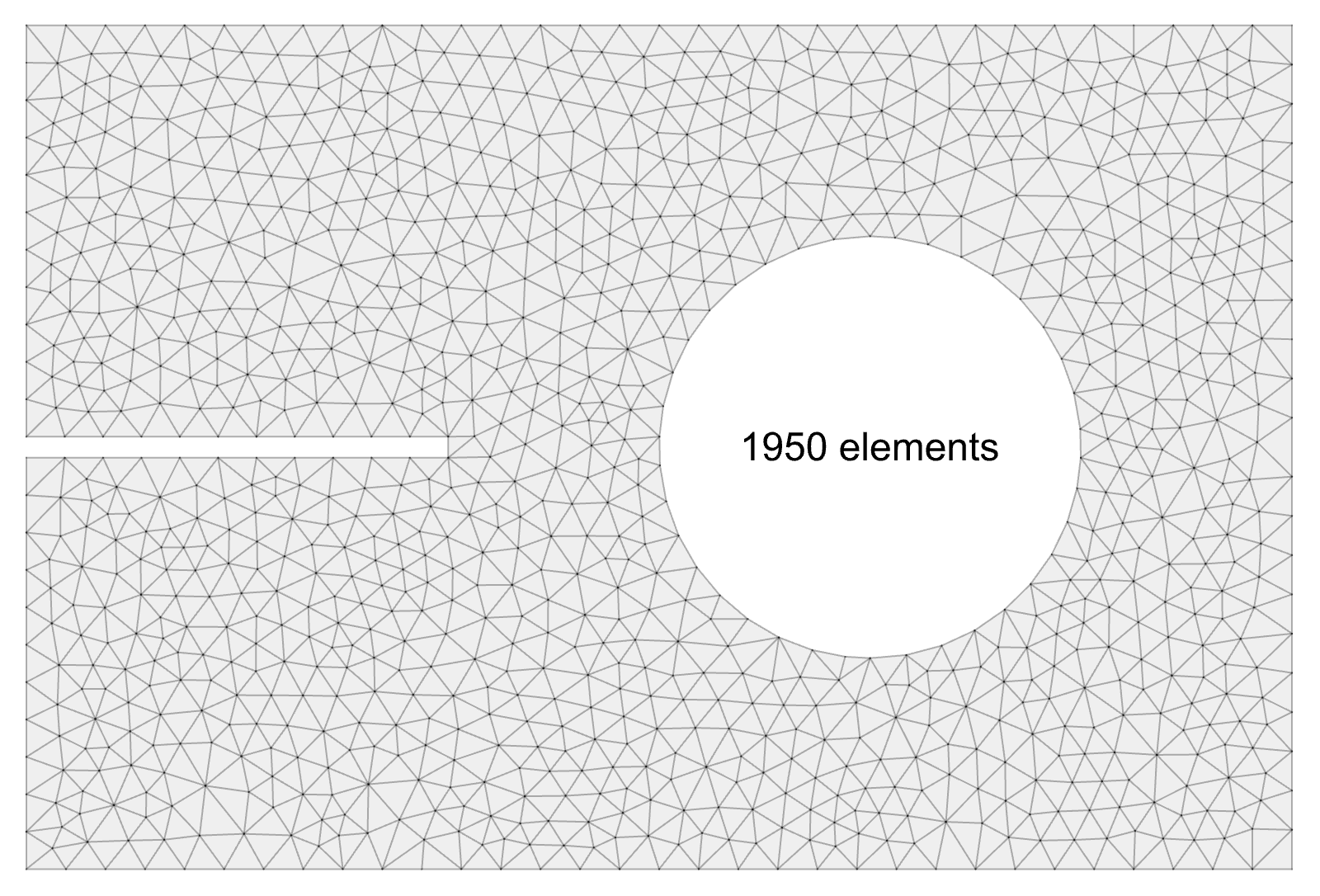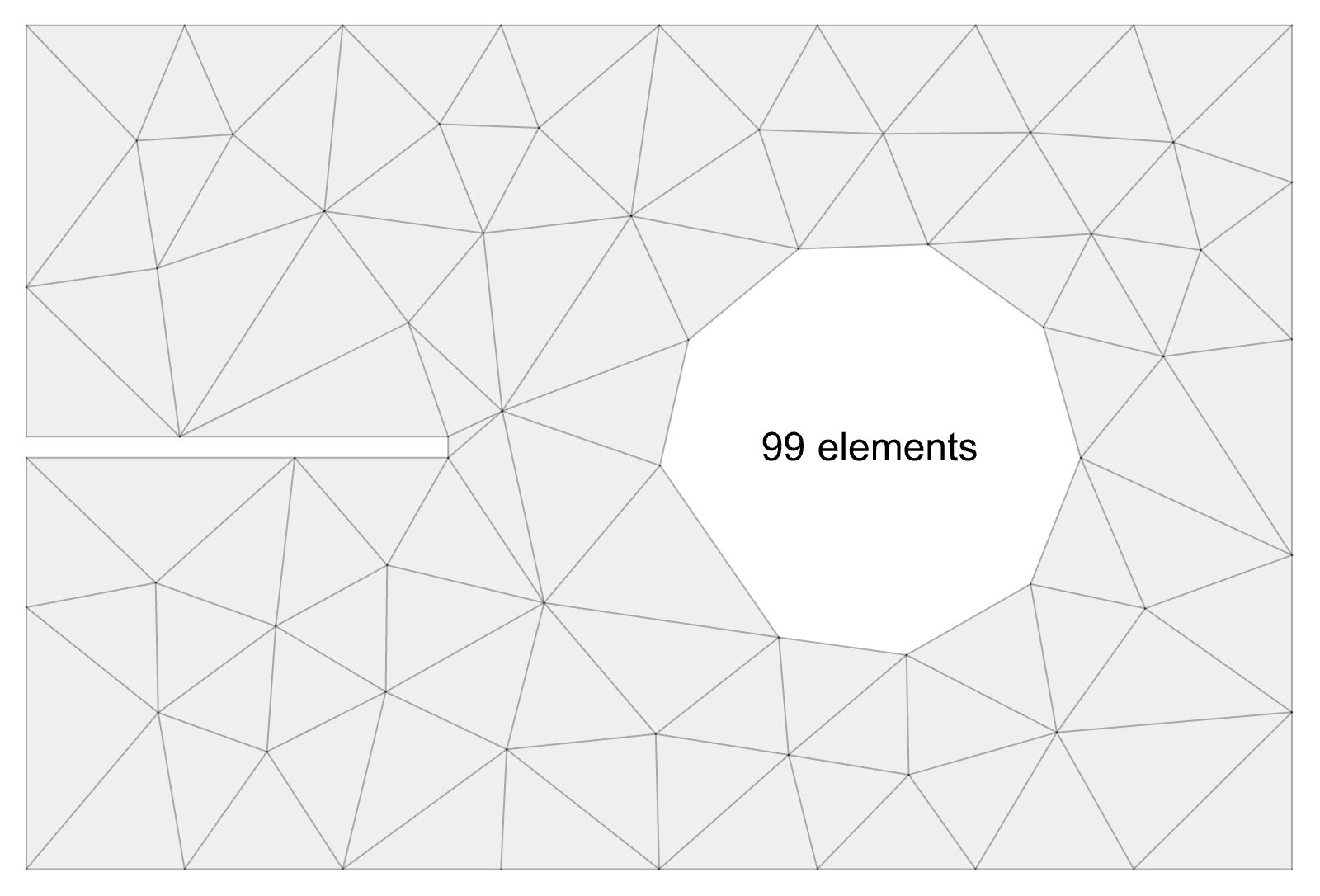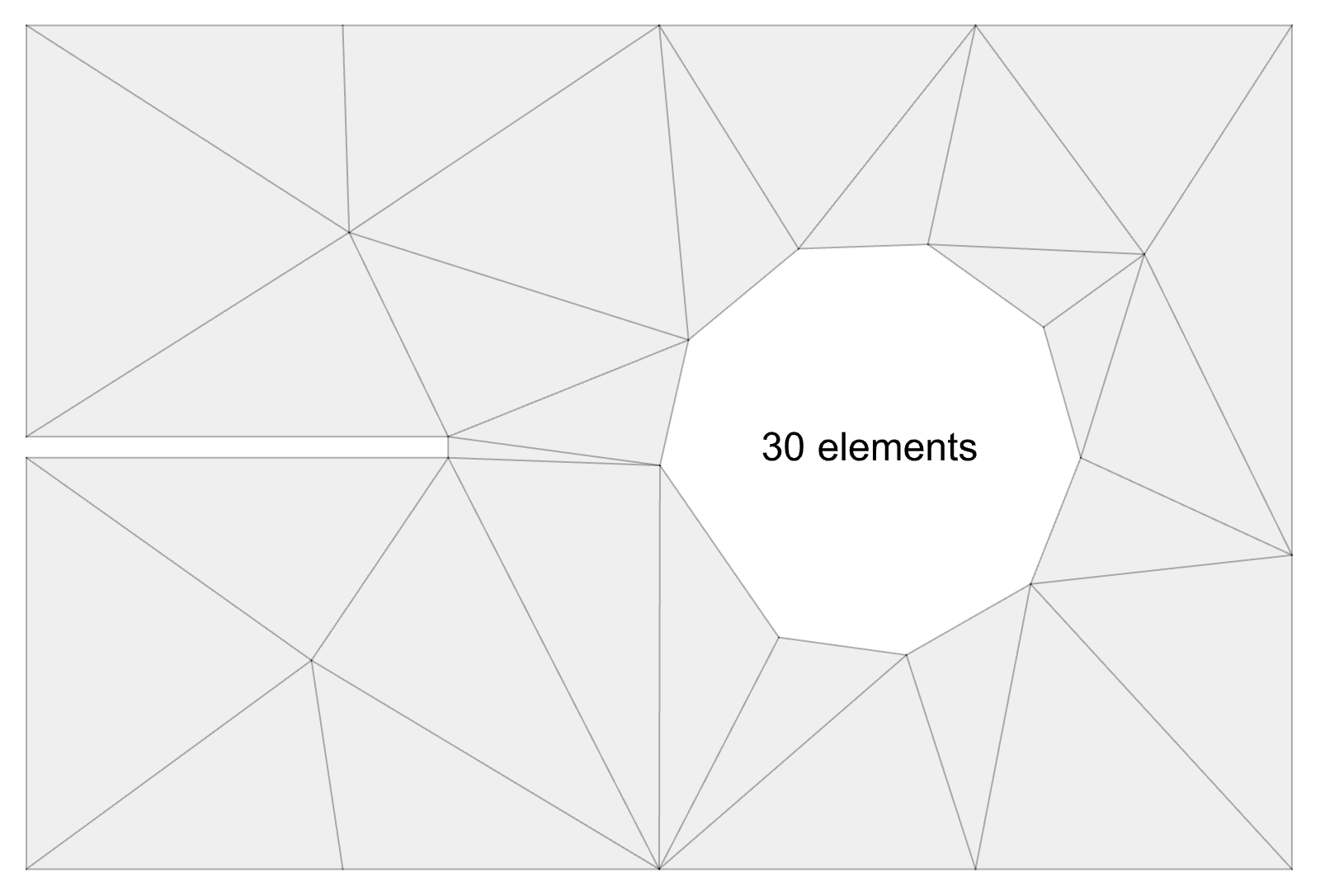
Examples:
Notched Plate with Hole:
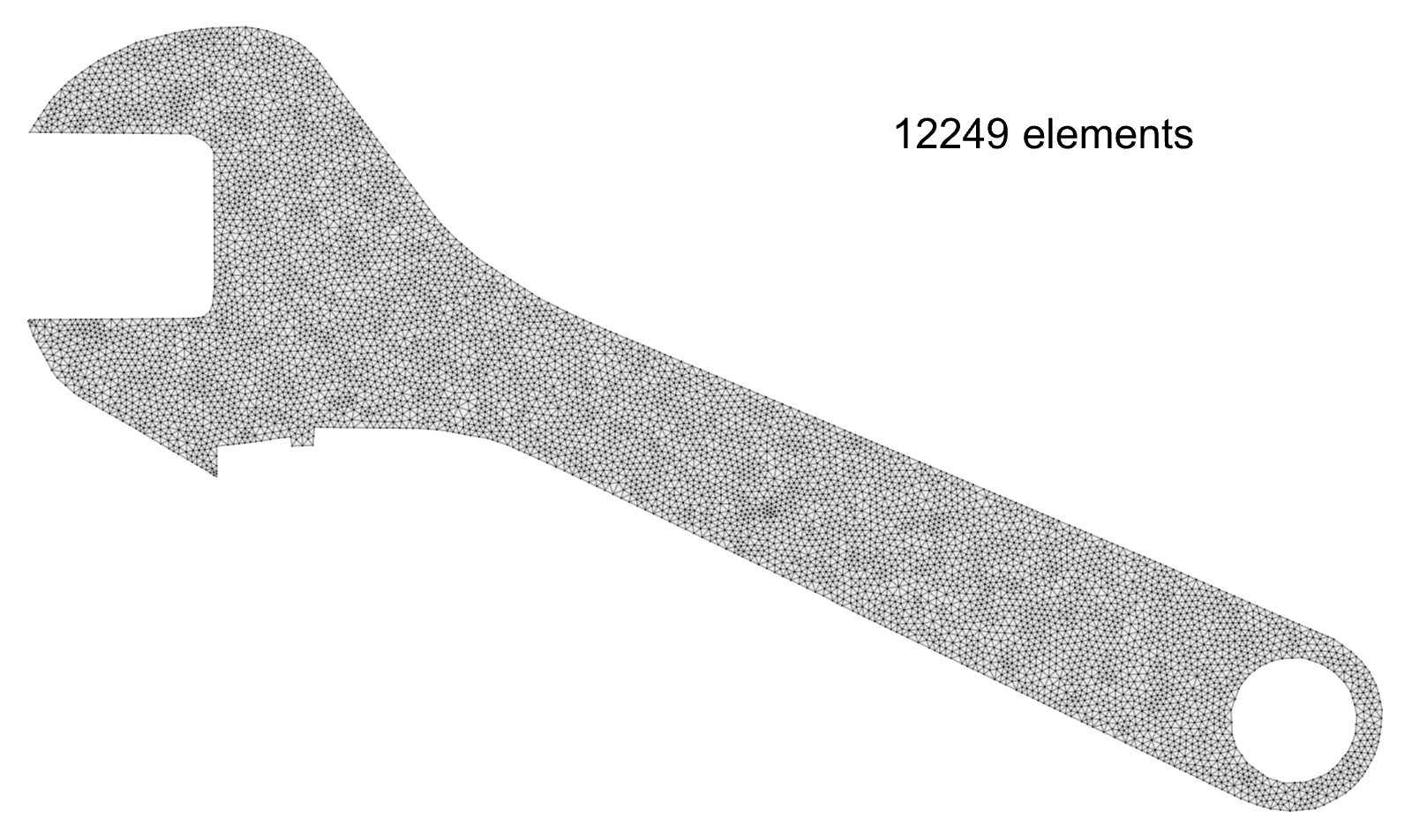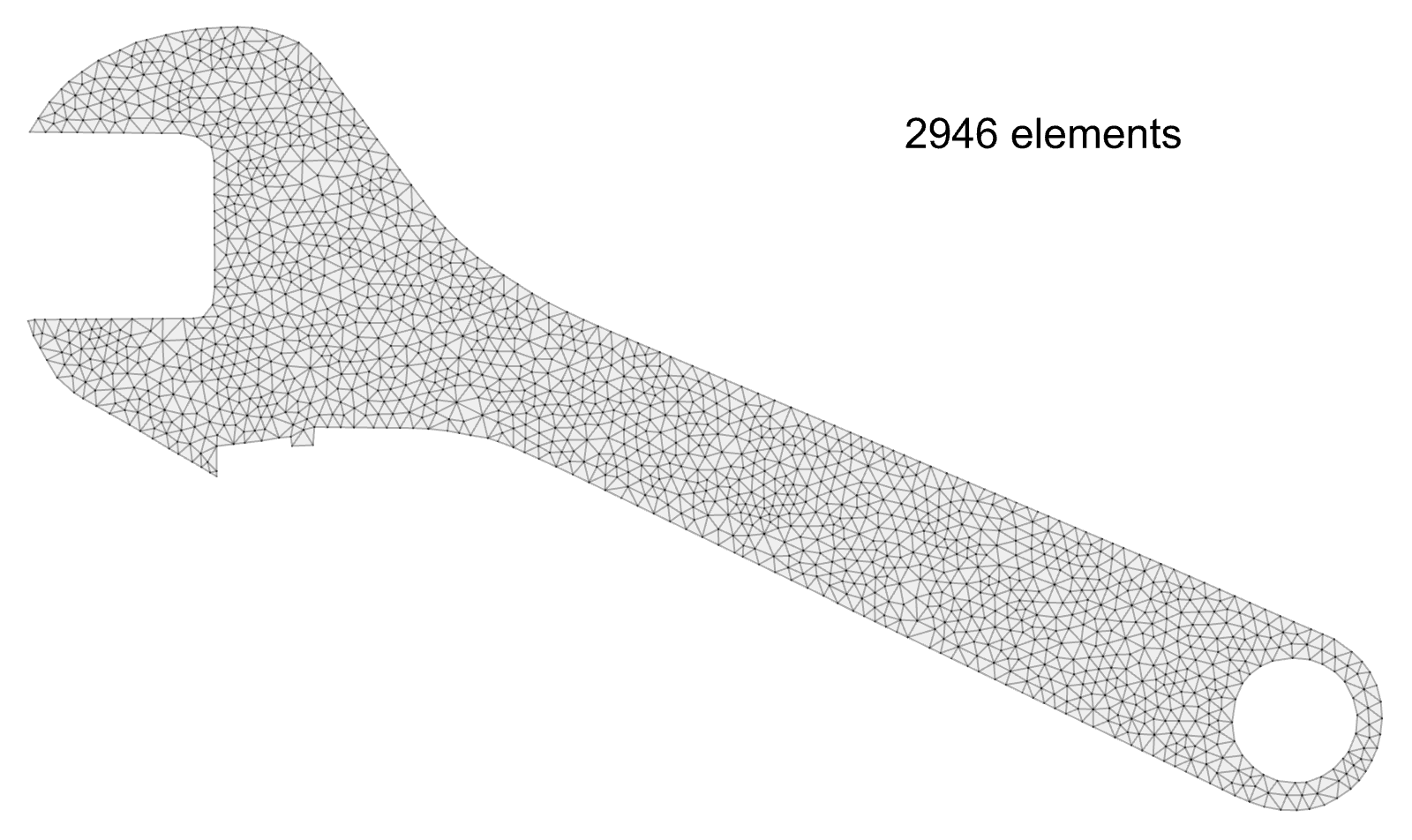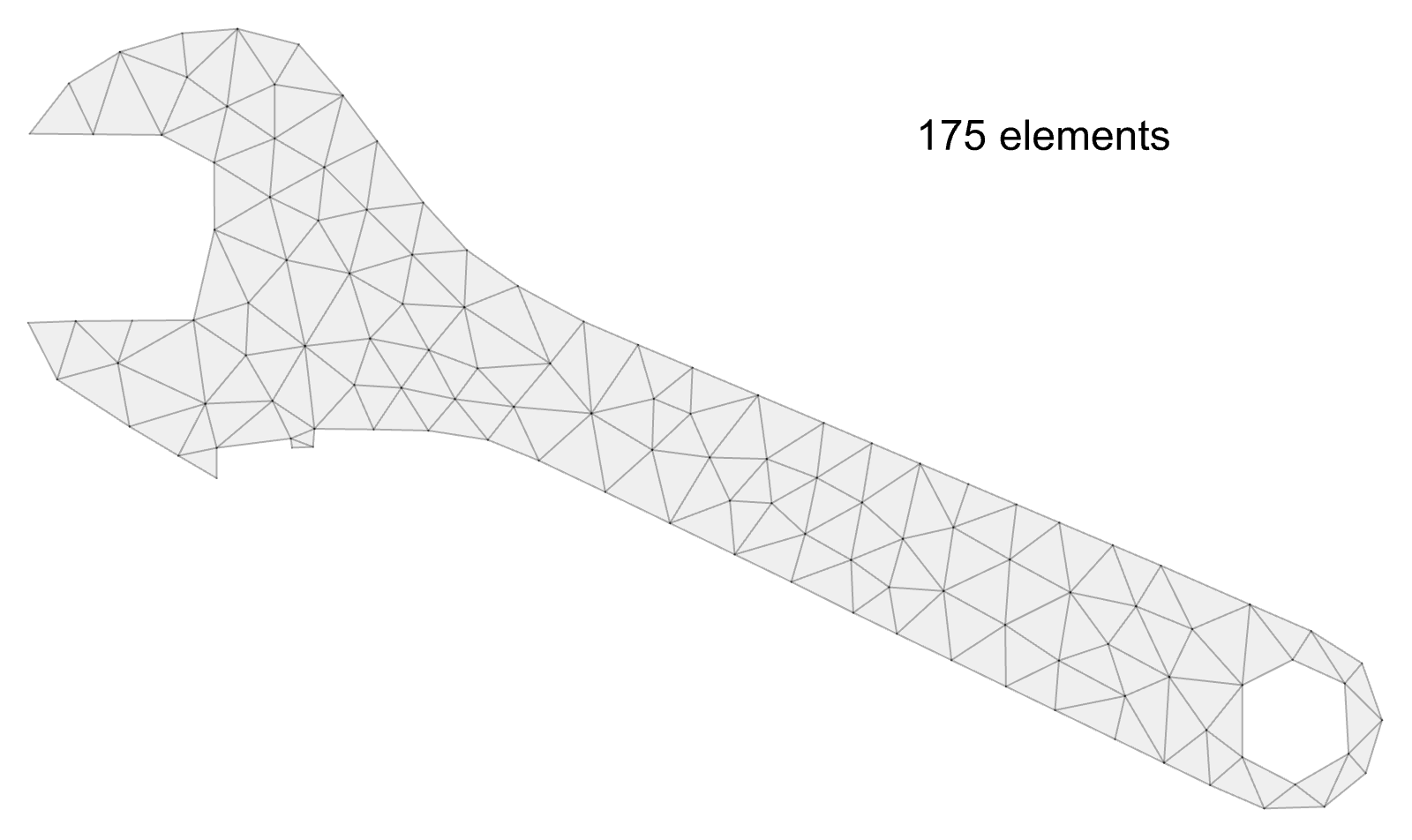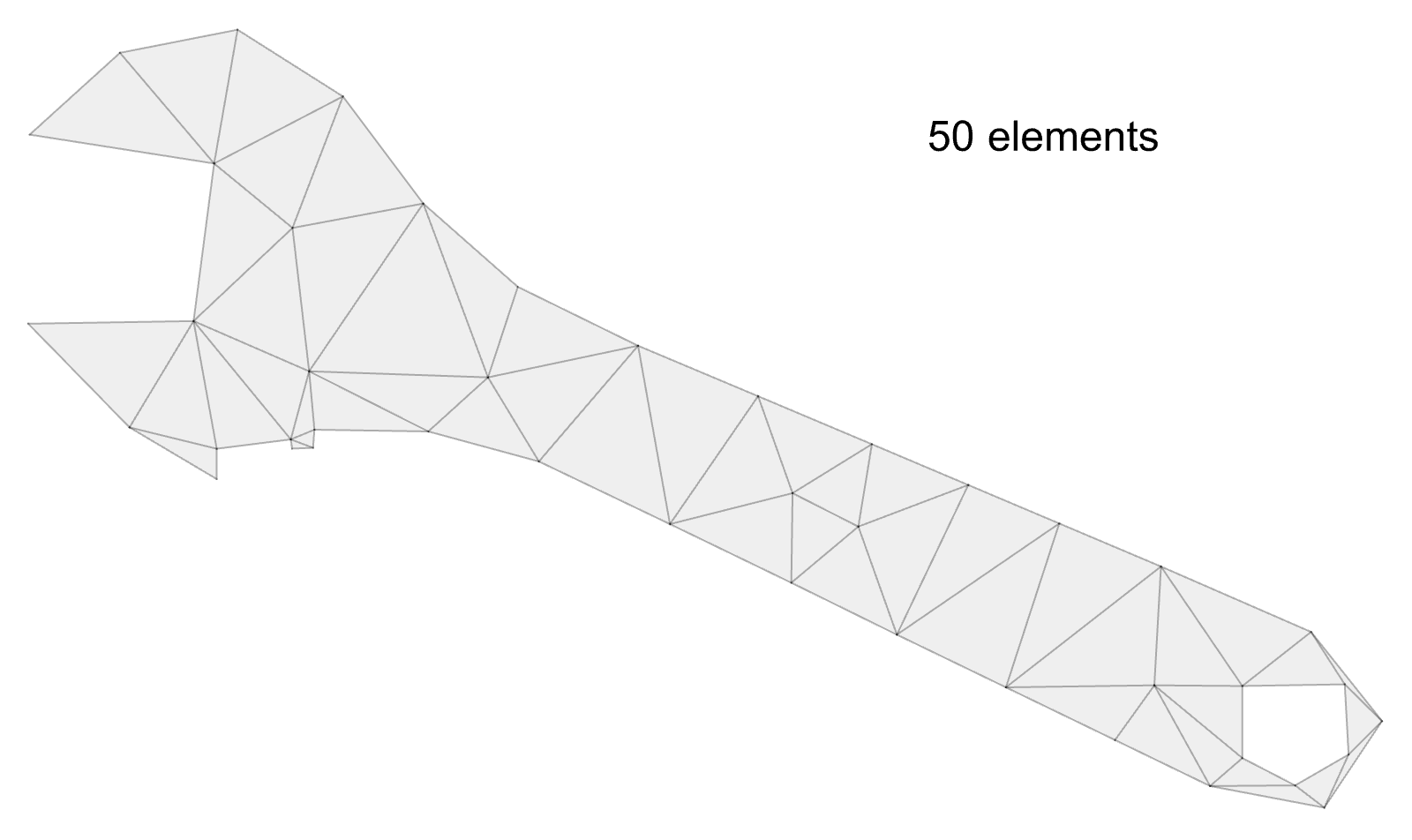
Wrench:
The C++ implementation used for all the examples in this document is available here.