Algebra

When we first learn about functions in algebra class, teachers often describe them as "black boxes" that transform inputs to outputs. This is usually accompanied by a picture of a box (representing the function) and some arrows (representing the inputs/outputs) like this,

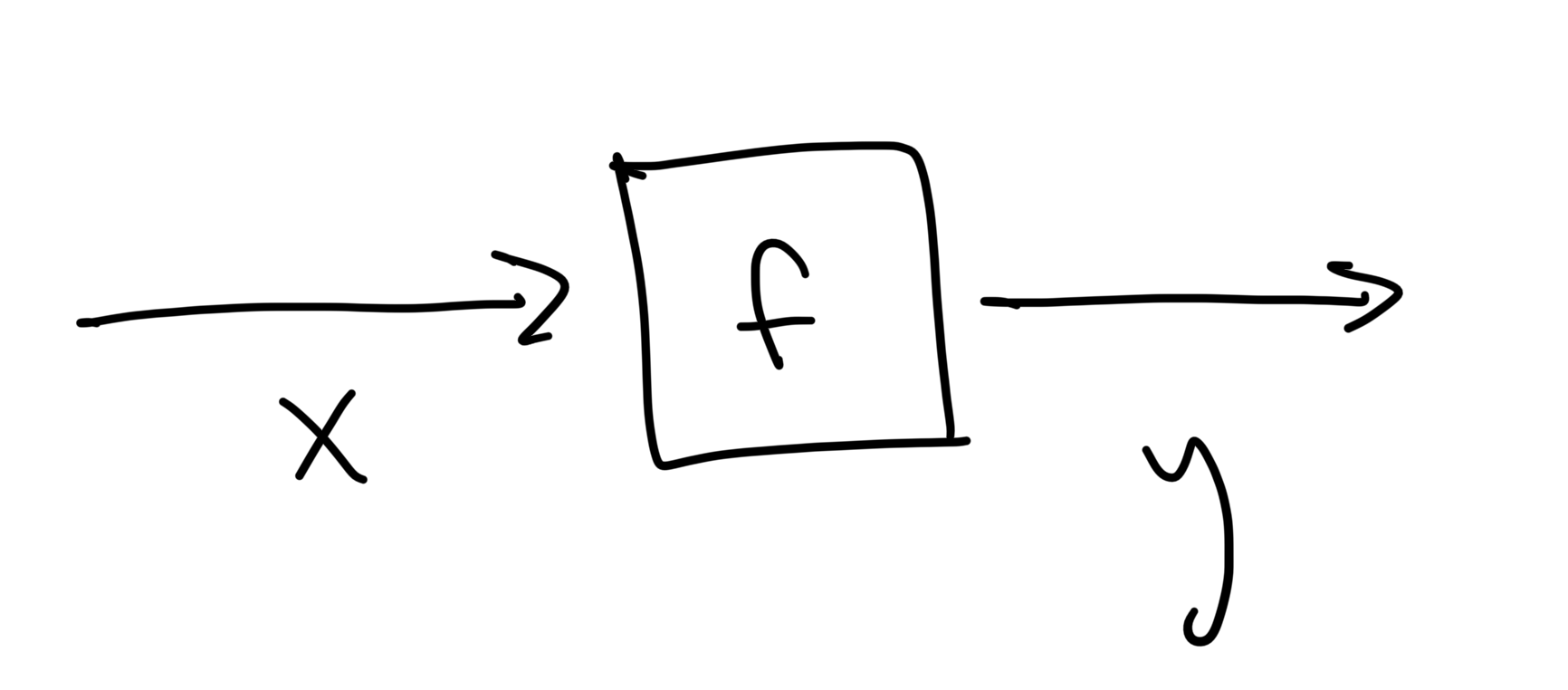
to help students make sense of the new abstract notation $y=f(x)$$y = f(x)$. After that, the following math classes tend to use the algebraic notation almost exclusively. However, in many cases the graph representation of calculations (where functions are nodes, and values are edges) is the more useful of the two.

In this document we'll cover how thinking about programs as graphs helps us understand and implement algorithmic differentiation.

Calculus

Several years after that algebra class we wind up taking calculus, where we study how small changes in the inputs, $dx$$dx$, effect small changes in the output of the function, $dy$$dy$. When these changes in the input are "small enough", then $dy$$dy$ and $dx$$dx$ are proportional to each other. The constant of proportionality, $\frac{dy}{dx}$$\frac{dy}{dx}$, gets a special name ("the derivative") and it lets us write

If we take that output $y$$y$ and feed it into another function, $g$$g$

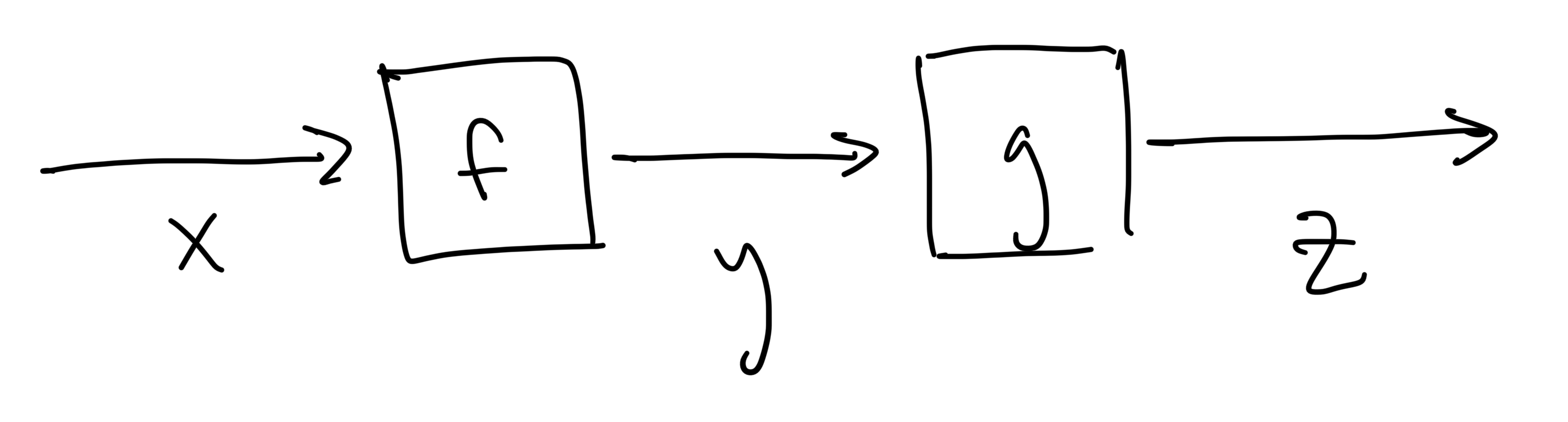
then the output $z$$z$ is (indirectly) a function of $x$$x$ as well: $z(x)=g(f(x))$$z(x) = g(f(x))$. The "Chain Rule" describes how to differentiate nested functions like this:

That is, the derivative of the composite function is the product of the derivatives of the individual steps.

Forward Mode Interpretation

Let's take that chain rule expression above, and multiply both sides of the equation above by $dx$$dx$ in order to write

From here, we can group certain terms together to keep track of the intermediate differential quantities

With all of the intermediate differential quantities accounted for now, we can draw a graph representation for them just like we did for the original calculation:

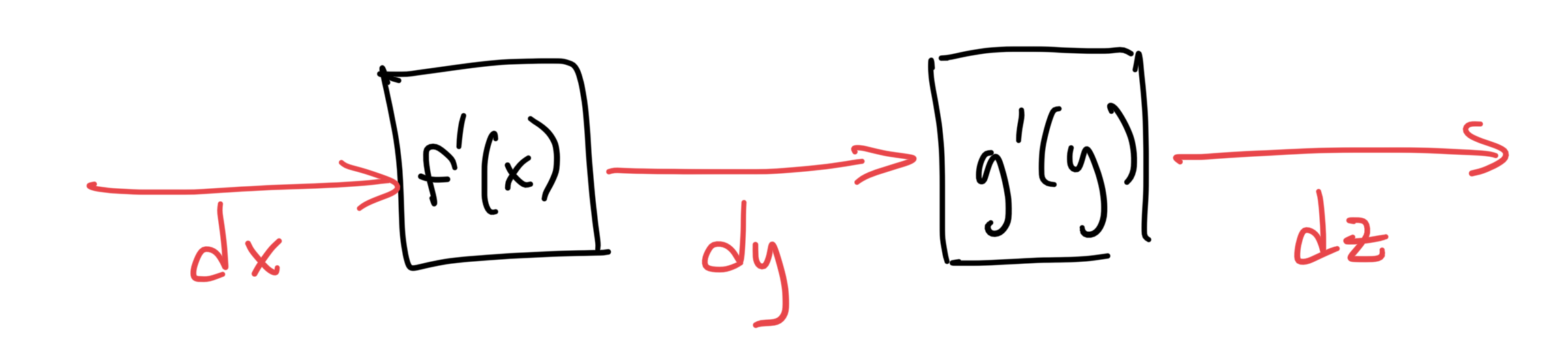
This is the graph associated with forward mode differentiation. There are a few important things to notice about it:

• the structure (node and edge connectivity) of the new graph is identical to the original graph

• the directions of the edges in the graph point the same direction as the original graph (hence, "forward" mode)

• the data carried by each edge in the new graph is the differential of its corresponding edge in the original graph

• the calculation performed at each node in the new graph is multiplication by the derivative of its corresponding calculation node in the original graph

If we want to compute the derivative of quantities w.r.t. $x$$x$, we can evaluate this graph with the input $dx=1$$dx = 1$ (or the appropriate identity element for more complicated types).

Reverse Mode Interpretation

Now let's go back to the chain rule equation and multiply both sides by $\frac{d◻}{dz}$$\frac{d\square}{dz}$ on the left, where $◻$$\square$ is some placeholder representing any possible quantity

Since this equation is the same for any such quantity $◻$$\square$, let's just leave it out of the expressions to make things a little more succinct.

Just like with the forward mode derivation, we'll group terms together. Except this time, let's see what happens when grouping terms from the left, rather than the right:

Again, this grouping of terms reveals information about the intermediate quantities. In this case, those intermediates are the derivatives w.r.t. edge data. I think this is easier to understand as a graph, so let's draw a picture

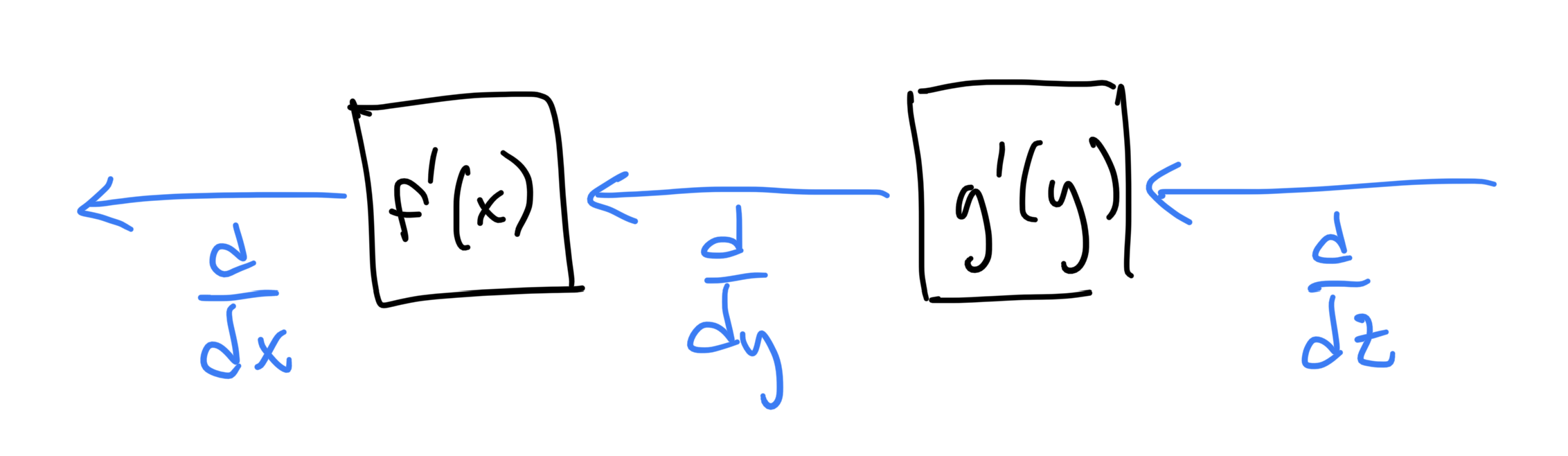
This is the graph associated with reverse mode differentiation (also referred to as "the adjoint method" and "backpropagation"). There are a few important things to notice about it:

• the structure (node and edge connectivity) of the new graph is almost identical to the original graph, except ...

• the directions of the edges in the graph point the opposite direction as the original graph (hence, "reverse" mode)

• the data carried by each edge in the new graph is the derivative w.r.t. its corresponding edge in the original graph

• the calculation performed at each node in the new graph is multiplication by the derivative of its corresponding calculation node in the original graph

If we want to compute the derivative of some quantity w.r.t. $x$$x$, we can evaluate this graph with the "input" derivative w.r.t. $z$$z$. If the quantity we want to differentiate is $z$$z$ itself, then we feed in $\frac{dz}{dz}=1$$\frac{dz}{dz} = 1$ as the input to the reverse mode graph.

Multivariable Calculus

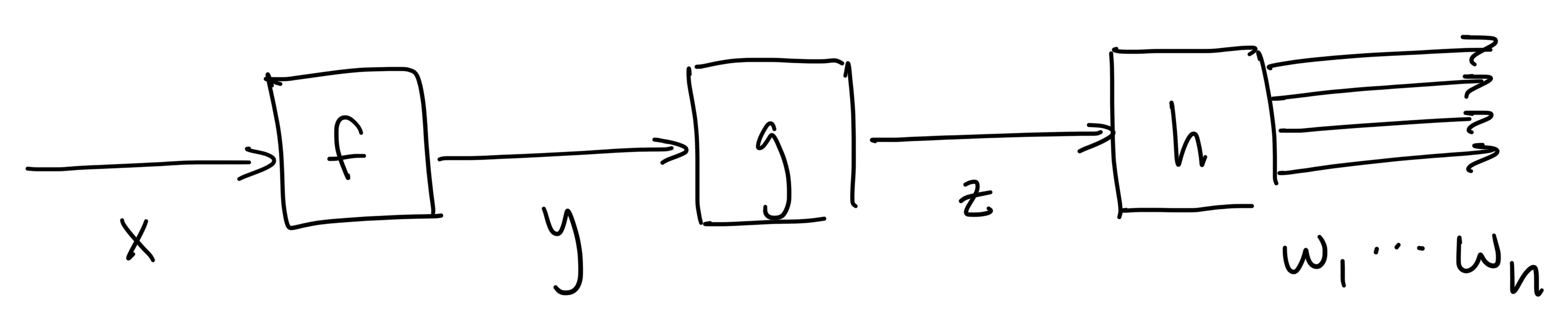
1D calculus is a good start, but in practice, calculations frequently involve functions with multiple inputs and outputs. So, let's briefly review how derivatives work for that case. For example, here's an arbitrary C++ function that has 2 inputs and 3 outputs:

std::array<double,3> f(double x1, double x2) {
  double y1 = sin(x1) + x2;
  double y2 = x1 - x2;
  double y3 = 3.0 * x2;
  return {y1, y2, y3};
}

In this case, there are a total of 6 independent partial derivatives: ${\displaystyle \frac{\partial y_1}{\partial x_1},\frac{\partial y_1}{\partial x_2},\frac{\partial y_2}{\partial x_1},\frac{\partial y_2}{\partial x_2},\frac{\partial y_3}{\partial x_1},\frac{\partial y_3}{\partial x_2}}$$\displaystyle \frac{\partial y_1}{\partial x_1}, \frac{\partial y_1}{\partial x_2}, \frac{\partial y_2}{\partial x_1}, \frac{\partial y_2}{\partial x_2}, \frac{\partial y_3}{\partial x_1}, \frac{\partial y_3}{\partial x_2}$.

Technically, partial derivatives use the $\partial$$\partial$ symbol instead $d$$d$, but for the rest of the document I'll just use $d$$d$ so all the notation on the graphs is consistent.

A natural way to arrange these partial derivatives is in a matrix (called the Jacobian) with as many rows as outputs and as many columns as inputs.

The reason for doing this is that it lets us use matrix multiplication notation to compactly represent both forward mode and reverse mode differentiation operations:

Forward mode: $\left[\begin{array}{c}d{y}_1\\ d{y}_2\\ d{y}_3\end{array}\right]=d\{y_1,y_2,y_3\}={\displaystyle \frac{d\{y_1,y_2,y_3\}}{d\{x_1,x_2\}}d\{x_1,x_2\}=\underset{{\displaystyle \mathbf{J}}}{\underbrace{\left[\begin{array}{cc}{\displaystyle \frac{d{y}_1}{d{x}_1}}& {\displaystyle \frac{d{y}_1}{d{x}_2}}\\ {\displaystyle \frac{d{y}_2}{d{x}_1}}& {\displaystyle \frac{d{y}_2}{d{x}_2}}\\ {\displaystyle \frac{d{y}_3}{d{x}_1}}& {\displaystyle \frac{d{y}_3}{d{x}_2}}\end{array}\right]}}\left[\begin{array}{c}d{x}_1\\ d{x}_2\end{array}\right]}$$\begin{bmatrix} dy_1 \\[0.75em] dy_2 \\[0.75em] dy_3 \end{bmatrix} = d\{y_1, y_2, y_3\} = \displaystyle \frac{d\{y_1, y_2, y_3\}}{d\{x_1, x_2\}} \; d\{x_1, x_2\} = \underbrace{\begin{bmatrix} \displaystyle \frac{dy_1}{dx_1} & \displaystyle \frac{dy_1}{dx_2} \\ \displaystyle \frac{dy_2}{dx_1} & \displaystyle \frac{dy_2}{dx_2} \\ \displaystyle \frac{dy_3}{dx_1} & \displaystyle \frac{dy_3}{dx_2} \end{bmatrix}}_{\displaystyle \bold{J}} \begin{bmatrix} dx_1 \\ dx_2 \end{bmatrix}$

Reverse mode: $\left[\begin{array}{cc}{\displaystyle \frac{d}{d{x}_1}}& {\displaystyle \frac{d}{d{x}_2}}\end{array}\right]={\displaystyle \frac{d}{d\{x_1,x_2\}}=\frac{d}{d\{y_1,y_2,y_3\}}\frac{d\{y_1,y_2,y_3\}}{d\{x_1,x_2\}}=\left[\begin{array}{ccc}{\displaystyle \frac{d}{d{y}_1}}& {\displaystyle \frac{d}{d{y}_2}}& {\displaystyle \frac{d}{d{y}_3}}\end{array}\right]\underset{{\displaystyle \mathbf{J}}}{\underbrace{\left[\begin{array}{cc}{\displaystyle \frac{d{y}_1}{d{x}_1}}& {\displaystyle \frac{d{y}_1}{d{x}_2}}\\ {\displaystyle \frac{d{y}_2}{d{x}_1}}& {\displaystyle \frac{d{y}_2}{d{x}_2}}\\ {\displaystyle \frac{d{y}_3}{d{x}_1}}& {\displaystyle \frac{d{y}_3}{d{x}_2}}\end{array}\right]}}}$$\begin{bmatrix} \displaystyle \frac{d}{d x_1} & \displaystyle \frac{d}{d x_2} \end{bmatrix} = \displaystyle \frac{d}{d\{x_1, x_2\}} = \frac{d}{d\{y_1, y_2, y_3\}} \; \frac{d\{y_1, y_2, y_3\}}{d\{x_1, x_2\}} = \begin{bmatrix} \displaystyle \frac{d}{dy_1} & \displaystyle \frac{d}{dy_2} & \displaystyle \frac{d}{dy_3} \end{bmatrix} \underbrace{\begin{bmatrix} \displaystyle \frac{dy_1}{dx_1} & \displaystyle \frac{dy_1}{dx_2} \\ \displaystyle \frac{dy_2}{dx_1} & \displaystyle \frac{dy_2}{dx_2} \\ \displaystyle \frac{dy_3}{dx_1} & \displaystyle \frac{dy_3}{dx_2} \end{bmatrix}}_{\displaystyle \bold{J}}$

Some AD libraries use the terms "JVP" and "VJP" as an alternate way of referring to forward and reverse mode, respectively. Those terms stand for "Jacobian-Vector Product" and "Vector-Jacobian Product", referring to whether the vector appears on the right or left of the Jacobian in the product.

More Complicated Example

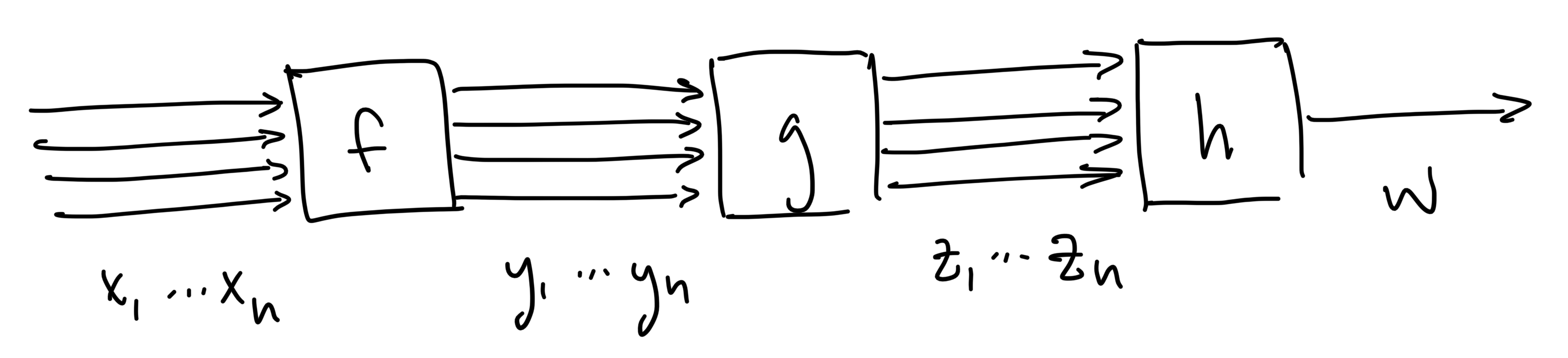
Let's apply our new intuition for forward and reverse mode differentiation to a slightly more involved calculation given in C++ below:

xxxxxxxxxx
double func(double x1, double x2) {
  auto [y1, y2] = f(x1, x2);
  double z = g(x1, y1);
  double w = h(z, y2);
  return w;
}

Start off by drawing the graph representation of the calculation, where edges are the variables and nodes are the calculations

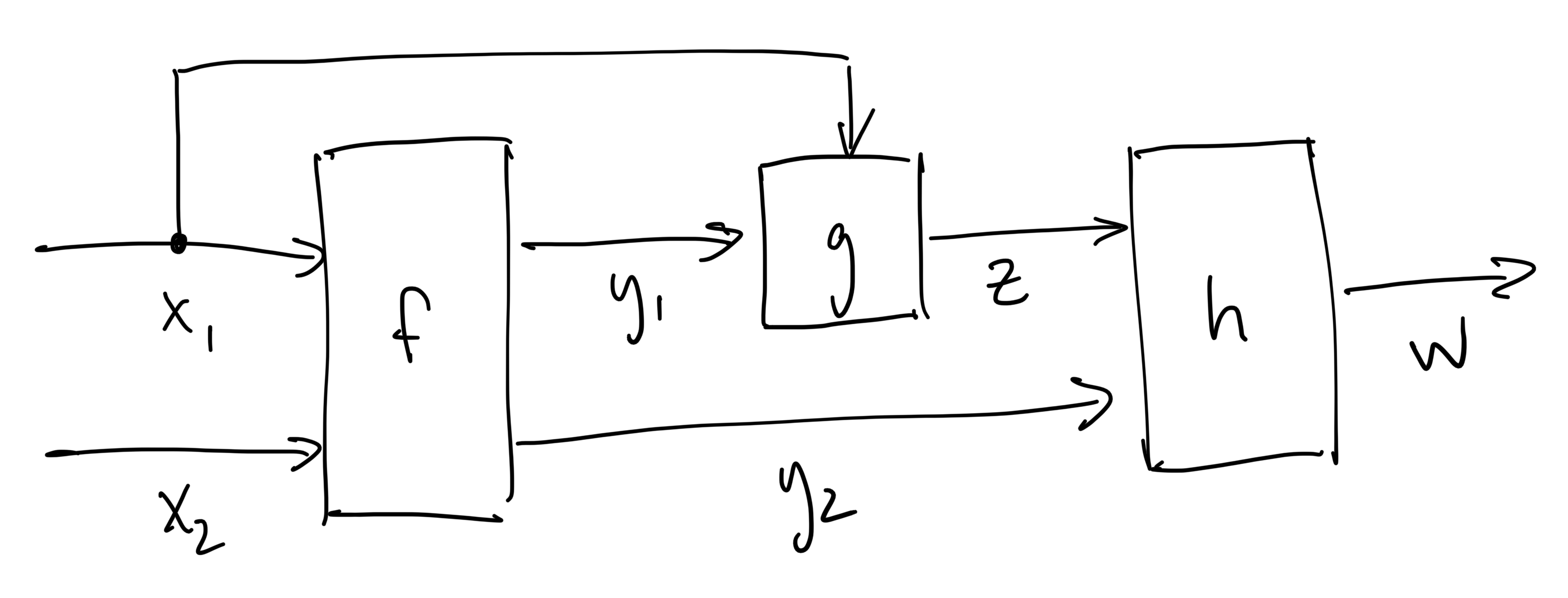
and then we can apply the rules we learned about forward and reverse mode from the earlier example.

Forward Mode

Recall that in order to make the graph for forward-mode, we replace each edge by a new edge carrying the differential of the original quantity and replace the nodes by their derivatives (evaluated at their respective function's inputs) to get:

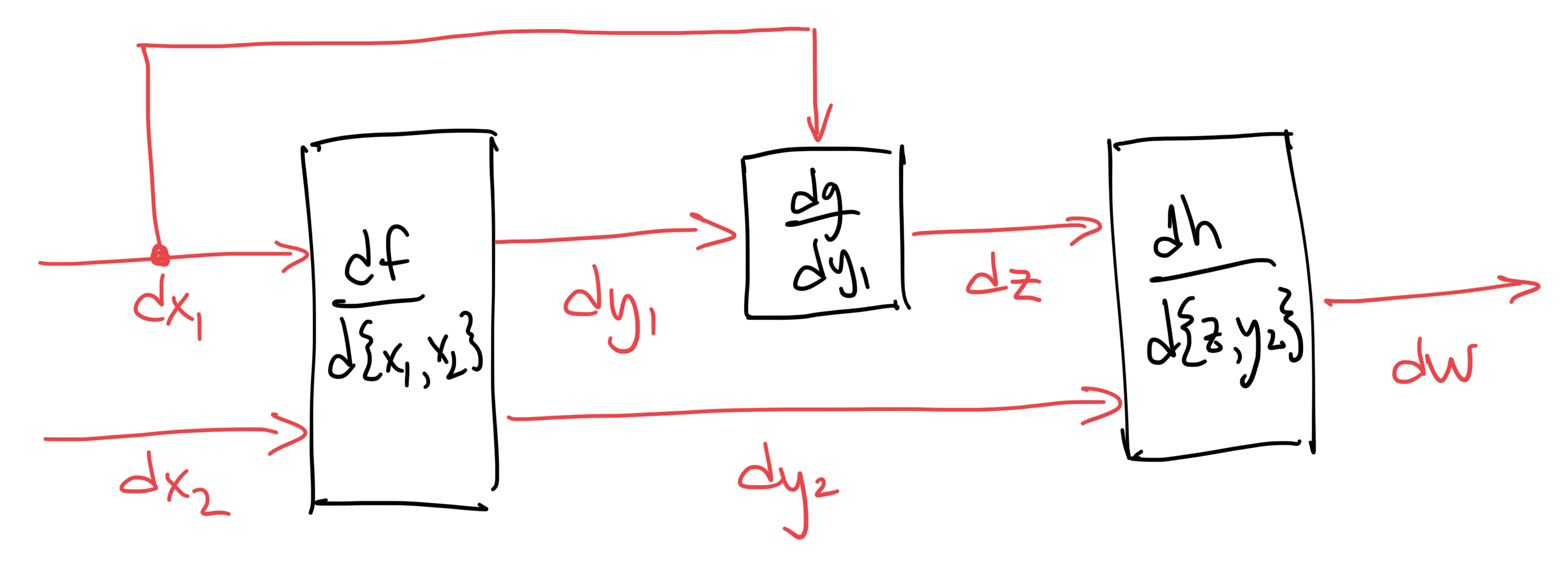
From here, we can compute different kinds of derivatives by feeding in different values for $d{x}_1,d{x}_2$$dx_1, dx_2$:

• to get the partial derivative ${\displaystyle \frac{\partial w}{\partial x_1}}$$\displaystyle \frac{\partial w}{\partial x_1}$, set $d{x}_1=1,d{x}_2=0$$dx_1 = 1, dx_2 = 0$

• to get the partial derivative ${\displaystyle \frac{\partial w}{\partial x_2}}$$\displaystyle \frac{\partial w}{\partial x_2}$, set $d{x}_1=0,d{x}_2=1$$dx_1 = 0, dx_2 = 1$

• to get a directional derivative, set $d{x}_1,d{x}_2$$dx_1, dx_2$ in the given direction

Reverse Mode

In reverse mode, we replace each edge by a new edge (in the opposite direction) that carries the derivative w.r.t. the original quantity and replace the nodes by their derivatives (evaluated at their respective function's inputs) to get:

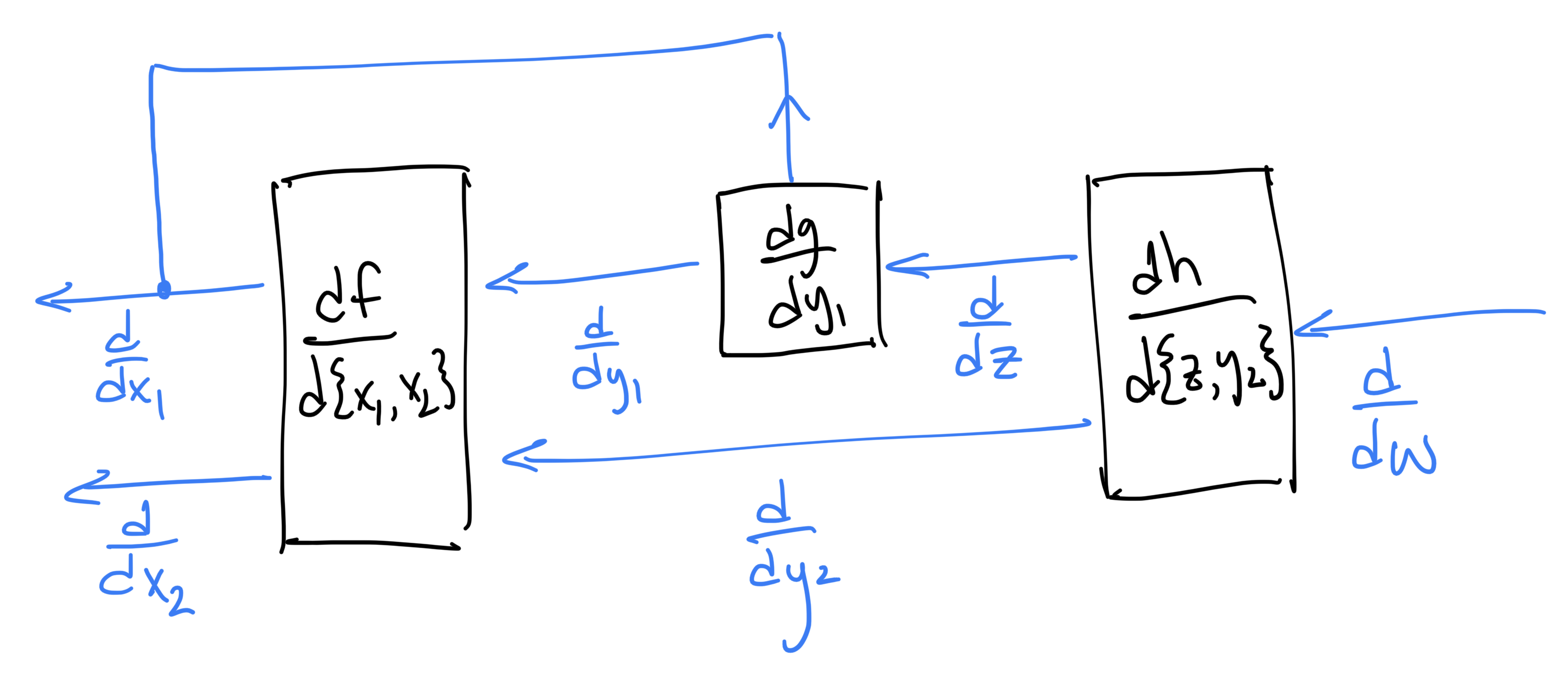
In reverse mode, if we provide a single value of $\frac{d◻}{dw}$$\frac{d\square}{dw}$ as the "input" (from the right), then when we carry out the calculations on this graph, we will have computed both $\frac{d◻}{d{x}_1},\frac{d◻}{d{x}_2}$$\frac{d\square}{dx_1}, \frac{d\square}{dx_2}$. This is different than forward-mode, which only gives a derivative w.r.t. one quantity at a time.

If we're after the quantities $\frac{dw}{d{x}_1},\frac{dw}{d{x}_2}$$\frac{dw}{dx_1}, \frac{dw}{dx_2}$, then we can just set $◻=w$$\square = w$, and pass in the number $1$$1$ as our input from the right.

Aside: Variable Reuse

If you were looking closely, you may have noticed that there was a small problem with the way I drew the graph for this "more complicated" example: the edge associated with input value $x_1$$x_1$ splits and goes off to two different functions. Technically, the edges in a graph should have a single starting point and a single endpoint. But in practice, that requirement feels awkward because programming languages have no problem letting you use a variable more than once.

The way I think about it is that drawings like the one below

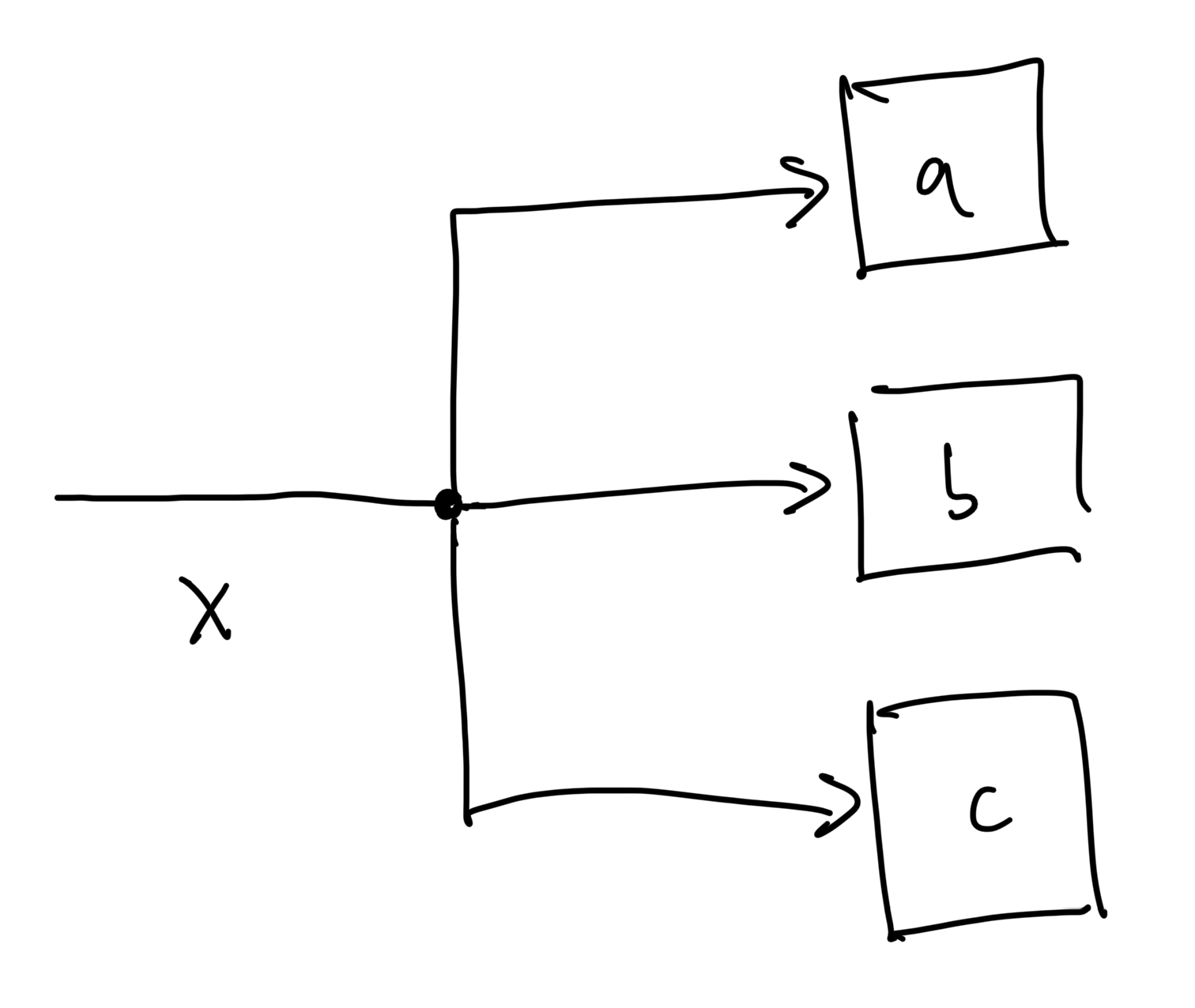
are really just a convenient short-hand notation for a more "proper" graph definition, where the splitting point is itself a node in the graph as well:

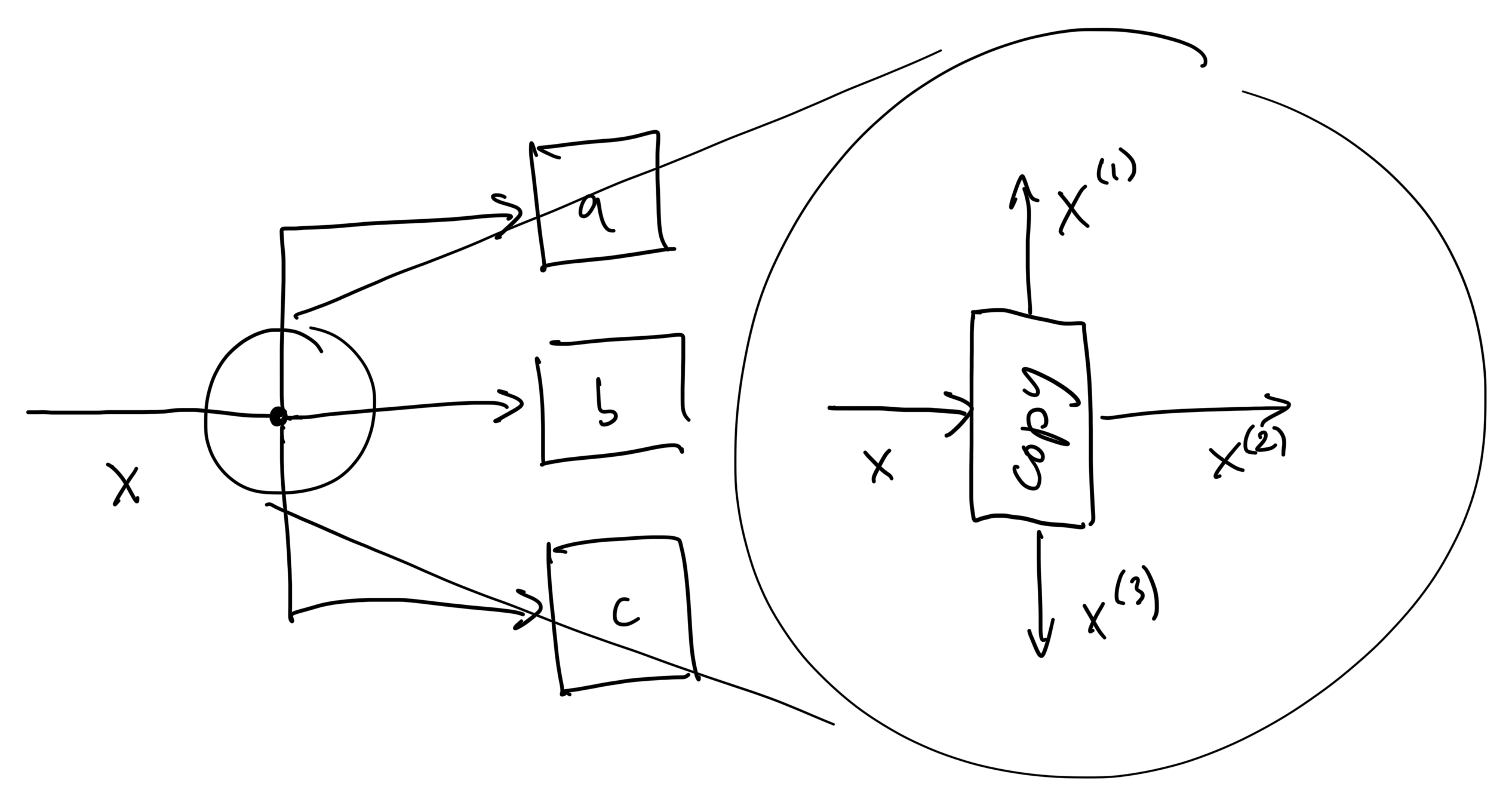
The actual calculation happening at that node is trivial: it's just copying the input value to the outputs. We could define this $\text{copy}$$\text{copy}$ function as

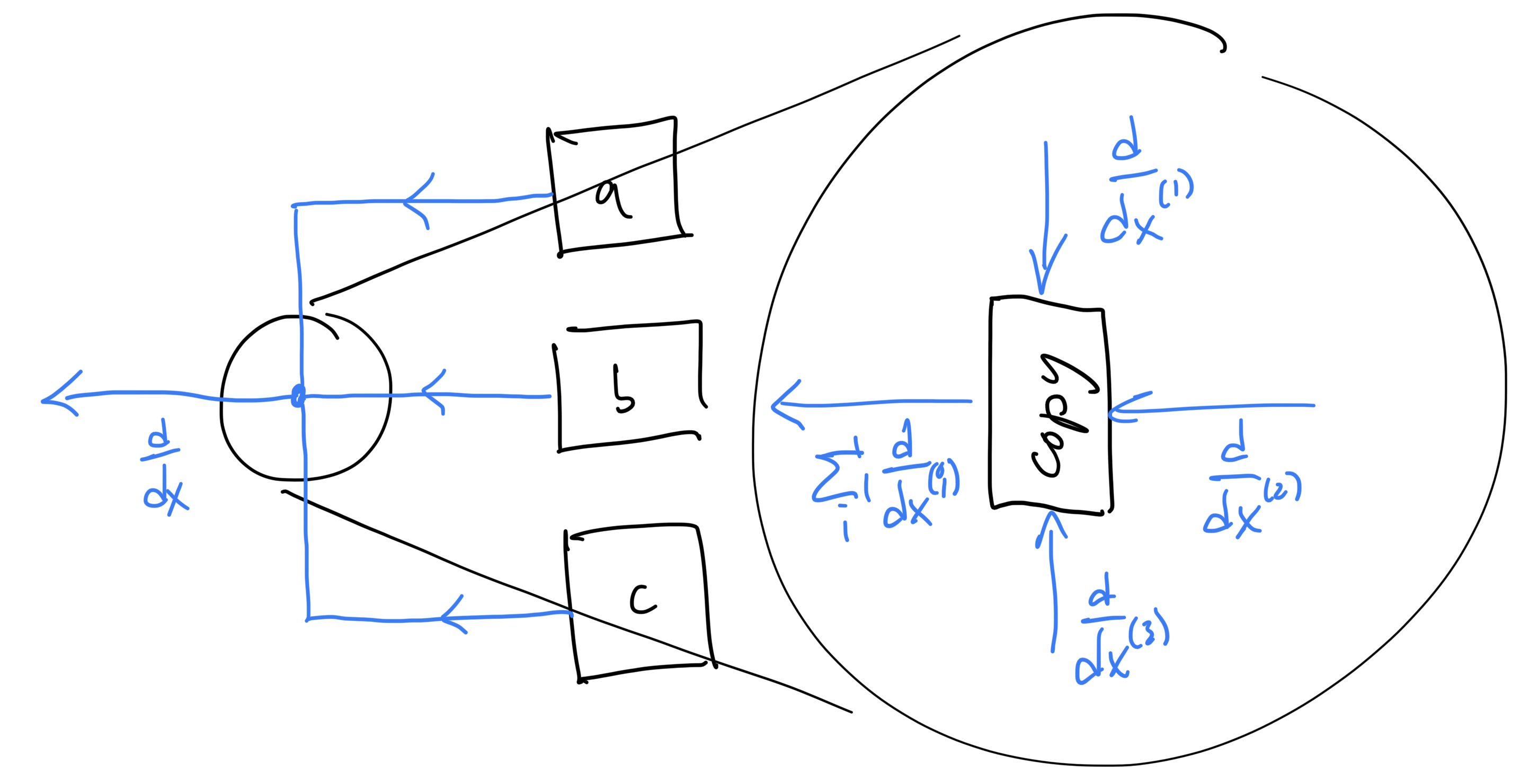
This way, our graph is still well-formed. This also has some implications for reverse-mode, since it means that, when visiting a $\text{copy}$$\text{copy}$ node on the reverse pass, we need to sum the relevant derivative terms:

Or, in graph form

When Should I Use Forward vs. Reverse Mode?

So far, we've only discussed how forward and reverse mode work, but haven't really described their strengths and weaknesses. Let's look at a couple specific examples to better understand the performance implications of forward vs. reverse mode.

Few Inputs, Many Outputs

Here is a graph featuring a scalar-valued input, scalar-valued intermediates and a vector-valued output.

For this graph, the chain rule tells us that ${\displaystyle \frac{d\{w_1,\cdots ,w_n\}}{dx}=\frac{d\{w_1,\cdots ,w_n\}}{dz}\frac{dz}{dy}\frac{dy}{dx}}$$\displaystyle \frac{d\{w_1, \cdots , w_n\}}{dx} = \frac{d\{w_1, \cdots , w_n\}}{dz} \; \frac{dz}{dy} \; \frac{dy}{dx}$.

Evaluating this expression with forward-mode means evaluating the products from right to left:

which involves multiplying two scalars ${\displaystyle \frac{dz}{dy}\frac{dy}{dx}}$$\displaystyle \frac{dz}{dy} \frac{dy}{dx}$ first ($1$$1$ op), and then multiplying a vector by a scalar ($n$$n$ ops) for a total of $n+1$$n+1$ operations. In contrast, reverse-mode evaluates the products from left to right:

That means first multplying a vector by a scalar ($n$$n$ ops), and then multiplying a vector by a scalar ($n$$n$ ops) for a total of $2n$$2n$ operations.

So, in this case where the size of the inputs/intermediates is smaller than the outputs, forward mode differentiation is preferred.

Many Inputs, Few Outputs

Here is another graph, except this one has a vector-valued input, vector-valued intermediates and a scalar-valued output.

For this graph, the chain rule tells us that ${\displaystyle \frac{dw}{d\{x_1,\cdots ,x_n\}}=\frac{dw}{d\{z_1,\cdots ,z_n\}}\frac{d\{z_1,\cdots ,z_n\}}{d\{y_1,\cdots ,y_n\}}\frac{d\{y_1,\cdots ,y_n\}}{d\{x_1,\cdots ,x_n\}}}$$\displaystyle \frac{dw}{d\{x_1, \cdots, x_n\}} = \frac{dw}{d\{z_1, \cdots, z_n\}} \; \frac{d\{z_1, \cdots, z_n\}}{d\{y_1, \cdots, y_n\}} \; \frac{d\{y_1, \cdots, y_n\}}{d\{x_1, \cdots, x_n\}}$.

Evaluating this expression with forward-mode performs the matrix-matrix multiplication on the right first (~$2n^3$$2n^3$ ops) and then a vector-matrix multiplication (~$2n^2$$2 n^2$ ops) for a total of about $2n^3$$2n^3$ operations.

With reverse mode, grouping from the left side leads to two vector-matrix products (~$2n^2$$2n^2$ ops, each) for a total of ~$4n^2$$4n^2$ operations. That is: for this kind of graph where there is a single output and many intermediates reverse mode is asymptotically faster by a factor of $n$$n$.

This kind of graph structure is extremely important, as it describes practically every optimization problem (since they typically involve many inputs variables and scalar-valued objective functions as the outputs). This also includes machine learning training workflows, which are essentially just big optimization problems.

This is the main reason that reverse-mode differentiation is such an important part of machine learning: forward mode would be incredibly slow for training.

Similar Number of Inputs, Intermediates, Outputs

In this case, the operation count of forward and reverse mode are roughly comparable. So, the tie is broken by the fact that forward-mode is generally simpler to implement and has a smaller memory footprint (since intermediate quantities can be discarded after use).

Summary

We covered a lot in this document, so let's recap some of the important ideas:

• representing programs and calculations as a graph clearly shows the flow of information and how the pieces fit together

• the graphs for forward and reverse mode differentiation are very similar to the graph of the original calculation

• The chain rule says that the derivative of a composite function is a product of individual derivatives

  • forward mode evaluates those products from right-to-left

  • reverse mode evaluates those products from left-to-right

  • it's also possible to mix and match forward/reverse for subgraphs and combine them

• forward mode

  • transforms small perturbations in the input into small perturbations in the output

  • flow of information follows the original program execution

  • good when # of inputs $\le$$\leq$ # of outputs

• reverse mode

  • transforms derivatives w.r.t. outputs into derivatives w.r.t. inputs

  • flow of information is opposite original program execution (requires a way to restore intermediates on reverse pass)

  • derivatives w.r.t. variables that are used in multiple places will have contributions from all the places they were used

  • good when # of outputs $\le$$\leq$ # of inputs (e.g. especially good for 1 output, like optimization)